题目内容
设F是抛物线C1：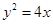
的焦点，点A是抛物线与双曲线C2：
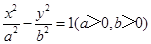的一条渐近线的一个公共点，且
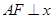轴，则双曲线的离心率为 ．
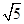
解析试题分析：抛物线C1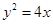：的焦点F（1，0)。
不妨设A为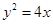 与
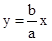的交点，∵AF⊥x轴，∴A(1，2)代入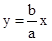得
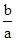=2，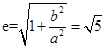
。
考点：本题主要考查抛物线、双曲线的几何性质。
点评：小综合题，涉及圆锥曲线的几何性质问题，多考查a,b,c,e,p的关系，要掌握几何元素之间的内再联系。本题若将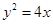化为更一般的
，也可得到类似结论。
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
+
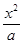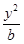=1(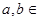
{1，2，3，4，…，2013})的曲线中，所有圆面积的和等于 ，离心率最小的椭圆方程为 .
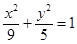的中心为顶点，右焦点为焦点的抛物线方程是 .
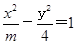的右焦点与抛物线
＝12x的焦点重合，则m＝______________．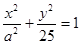
(
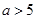),它的两个焦点分别为
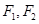,且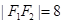
,弦AB(椭圆上任意两点的线段)过点
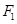,则
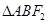的周长为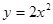 
的焦点坐标是_______________． 
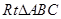中，
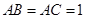，以点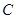
为一个焦点作一个椭圆，使这个椭圆的另一焦点在
边上，且这个椭圆过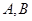
两点，则这个椭圆的焦距长为 ．
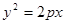的焦点与双曲线
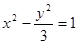的右焦点重合，则
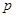的值为 ．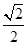
围成的三角形区域(包含边界)为E，P(x，y)为该区域的一个动点，则目标函数z＝x－2y的最小值为________．