题目内容
设a为实常数,已知函数![]() 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且![]() 在区间[0,1]上是减函数。
在区间[0,1]上是减函数。
(Ⅰ)求常数![]() 的值;
的值;
(Ⅱ)设点P为函数![]() 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线![]() 距离的最小值;
距离的最小值;
(Ⅲ)若当![]() 且
且![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
(Ⅰ) ![]()
(Ⅱ)![]()
(Ⅲ)(-∞,1]
解析:
(Ⅰ)因为![]() 在区间[1,2]上是增函数,则
在区间[1,2]上是增函数,则
当x∈[1,2]时,![]() 恒成立,即
恒成立,即![]() 恒成立,所以
恒成立,所以![]() 。 (2分)
。 (2分)
又![]() 在区间[0,1]上是减函数,则
在区间[0,1]上是减函数,则
当x∈(0,1]时,![]() 恒成立,即
恒成立,即![]() 恒成立,所以
恒成立,所以![]() 。
。
综上分析,![]() 。 (4分)
。 (4分)
(Ⅱ)因为![]() ,则
,则![]() 。
。
令![]() ,则
,则![]() ,
,![]() 。
。
所以函数![]() 图象上点
图象上点![]() 处的切线与直线
处的切线与直线![]() 平行。 (6分)
平行。 (6分)
设所求距离的最小值为d,则d为点![]() 到直线
到直线![]() 的距离,
的距离,
故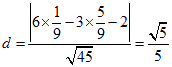 。 (8分)
。 (8分)
(Ⅲ)因为![]() ,则
,则![]() 。因为当
。因为当![]() 时,
时,![]() ,所以
,所以![]() 在(0,1]上是减函数,从而
在(0,1]上是减函数,从而![]() 。 (9分)
。 (9分)
因为当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 。 (10分)
。 (10分)
又当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 在
在![]() 时恒成立。 (11分)
时恒成立。 (11分)
因为![]() 在
在![]() 时是减函数,所以
时是减函数,所以![]() ,从而
,从而![]() ,即
,即![]() 。
。
故b的取值范围是(-∞,1]。 (13分)

练习册系列答案
相关题目