题目内容
对于函数![]() ,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直。
,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直。
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若关于![]() 的方程
的方程![]() 有三个不等实根,求实数
有三个不等实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 无零点,求实数
无零点,求实数![]() 的取值范围。
的取值范围。
(Ⅰ)![]()
(Ⅱ)![]()
(Ⅲ)![]()
解析:
(Ⅰ)![]() 。 (1分)
。 (1分)
据题意,当![]() 时
时![]() 取极值,所以
取极值,所以![]() 。 (2分)
。 (2分)
因为![]() ,由1-2a=0,得
,由1-2a=0,得![]() 。 (4分)
。 (4分)
(Ⅱ)因为![]() ,则
,则![]() ,
,
所以![]() 。
。
由![]() ,得
,得![]() ,即x<-1或1<x<2。
,即x<-1或1<x<2。
所以f(x)在区间![]() ,(1,2)上单调递增,在区间(-1,1),(2,+∞)上单调递减。(6分)
,(1,2)上单调递增,在区间(-1,1),(2,+∞)上单调递减。(6分)
所以![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() 。 (7分)
。 (7分)
由此可得函数y=f(x)的大致图象如下: (8分)
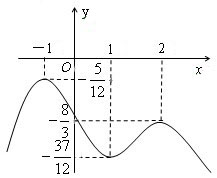
令![]() ,若关于
,若关于![]() 的方程
的方程![]() 有三个不等实根,
有三个不等实根,
则关于![]() 的方程
的方程![]() 在
在![]() 上有三个不等实根,
上有三个不等实根,
即函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有三个不同的交点。
上有三个不同的交点。
又![]() ,由图象可知,
,由图象可知,![]() ,
,
故![]() 的取值范围是
的取值范围是![]() 。 (9分)
。 (9分)
(Ⅲ)若函数![]() 无零点,则当
无零点,则当![]() 时,
时,![]() 。
。
设函数![]() 的定义域为D,则当x∈D时,恒有
的定义域为D,则当x∈D时,恒有![]() 或
或![]() 。(11分)
。(11分)
因为函数![]() 的值域是
的值域是![]() ,所以
,所以![]() ,即
,即![]() 。
。
故p的取值范围是![]() 。 (13分)
。 (13分)

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
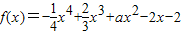 ,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.
,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.