题目内容
本小题满分15分）已知
R，函数.（
R，e为自然对数的底数）
（1）当a=-2时，求函数f(x)的单调递减区间；
（2）若函数f(x)在（-1,1）内单调递减，求a的取值范围；
（3）函数f(x)是否为R上的单调函数，若是，求出a的取值范围；若不是，请说明理由.
【答案】
对
都成立.…………………………………7分
令
，则
………………………………………………………………………9分
. （注：不带等号扣1分） …………………………………………10分
（Ⅲ）①若函数
在R上单调递减，则
对
R 都成立
即
对R都成立.…………………………10分
对R都成立………………………11分
令，
图象开口向上 
不可能对R都成立
………………………………12分
②若函数在R上单调递增，则
对R 都成立，
即
对R都成立，
对R都成立.………………13分
故函数不可能在R上单调递增.……………………………………14分
综上可知，函数不可能是R上的单调函数 …………………15分
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
。
成立的
的取值范围；
的最小值。
为
的极值点，求实数
的值；
在
上为增函数，求实数
时，方程
有实根，求实数
的取值范围。
，
，直线
与函数
、
的图象都相切，且与函数
.
的值；
(其中
是
的最大值；
时，求证：
.
。
的图象有与
轴平行的切线，求
的取值范围；
时取得极值，且
时，
恒成立，求
的取值范围。
过点(1, 
)，F1、F2分别为其左、右焦点,且离心率e=
的直线
与椭圆C交于不同的两点
、
，且∠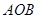
为锐角（其中
为坐标原点），求直线
的取值范围.