题目内容
(本题14分)数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 总有
总有 成等差数列。
成等差数列。
(1)求 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,且
,且 ,求证对任意的实数
,求证对任意的实数 和任意的整数
和任意的整数 总有
总有 ;
;
(3)正数数列 中,
中,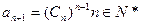 ,求数列
,求数列 的最大项。
的最大项。
 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 总有
总有 成等差数列。
成等差数列。(1)求
 的通项公式;
的通项公式;(2)设数列
 的前
的前 项和为
项和为 ,且
,且 ,求证对任意的实数
,求证对任意的实数 和任意的整数
和任意的整数 总有
总有 ;
;(3)正数数列
 中,
中,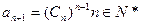 ,求数列
,求数列 的最大项。
的最大项。(1)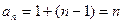 (2)略(3)
(2)略(3)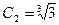
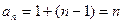 (2)略(3)
(2)略(3)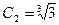
解:(1)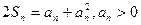
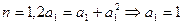
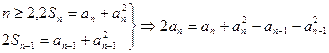
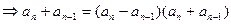
又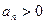
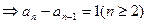
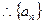 是公差为1的等差数列,
是公差为1的等差数列,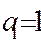
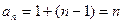 …………………………………………………………4分
…………………………………………………………4分
(2)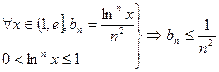
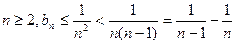
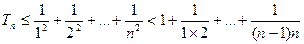

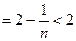 ……………………………………………………………………8分
……………………………………………………………………8分
(3)已知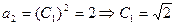
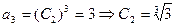
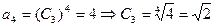
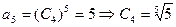
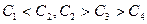 ,猜想
,猜想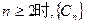 递减 ……………………10分
递减 ……………………10分
令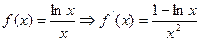
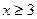 是
是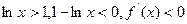
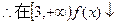
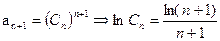
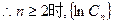 是递减数列
是递减数列
即 是递减数列
是递减数列
又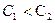 ,故
,故 最大项为
最大项为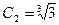 …………………………14分
…………………………14分
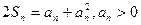
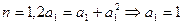
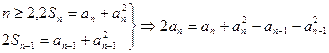
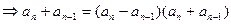
又
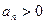
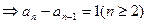
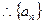 是公差为1的等差数列,
是公差为1的等差数列,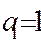
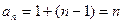 …………………………………………………………4分
…………………………………………………………4分(2)
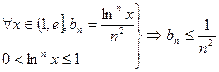
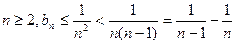
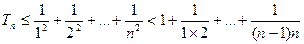

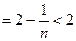 ……………………………………………………………………8分
……………………………………………………………………8分(3)已知
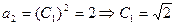
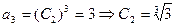
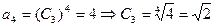
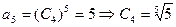
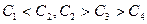 ,猜想
,猜想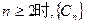 递减 ……………………10分
递减 ……………………10分令
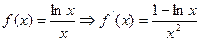
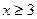 是
是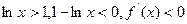
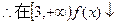
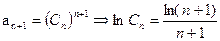
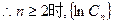 是递减数列
是递减数列即
 是递减数列
是递减数列又
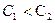 ,故
,故 最大项为
最大项为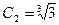 …………………………14分
…………………………14分
练习册系列答案
相关题目
 .
. 满足:
满足:

 中,
中,
 , 则
, 则
 =" " .
=" " . 在
在 处连续,则
处连续,则 ( )
( )

 的前
的前 项和分别为
项和分别为 ,若
,若 ,则
,则 ( ).
( ).


