题目内容
设函数 的定义域为
的定义域为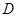 ,若存在非零实数
,若存在非零实数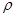 ,使得对于任意
,使得对于任意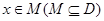 ,有
,有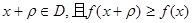 ,则称
,则称 为
为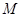 上的
上的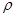 高调函数,若定义域是
高调函数,若定义域是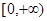 的函数
的函数 为
为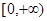 上的
上的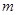 高调函数,则实数m的取值范围是 .
高调函数,则实数m的取值范围是 .
【答案】

【解析】
试题分析:因为定义域是[0,+∞)的函数f(x)=(x-1)2为[0,+∞)上的m高调函数,
由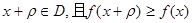 ,得当x=0得到f(m)≥f(0)即(m-1)2≥1,
,得当x=0得到f(m)≥f(0)即(m-1)2≥1,
解得m≥2或m≤0(又因为函数的定义域为[0,+∞)所以舍去),
所以m∈[2,+∞),故答案为[2,+∞)
考点:本试题主要考查学生理解函数恒成立时取条件的能力,以及用特值法解题的能力,解一元二次不等式的能力,考查了分析问题和解决问题的能力。
点评:解决该试题的关键是理解何为高调函数,并能理解m高调函数的意思就是使得f(m)≥f(0),进而通过特殊点的分析解得。

练习册系列答案
相关题目
 的定义域为
的定义域为 ,若满足:①
,若满足:①
 ,使得
,使得 上的值域为
上的值域为 是定义域为
是定义域为 是定义域为
是定义域为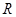 的“成功函数”,则
的“成功函数”,则 的取值范围为 ( )
的取值范围为 ( )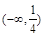 B.
B.
 C.
C.
 D.
D.

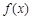 的定义域为
的定义域为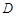 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
; 的定义域为
的定义域为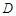 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
;