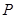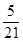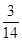题目内容
(本小题满分12分)
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)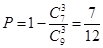 ;
;
(Ⅱ) .
.
(Ⅲ) 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
 的数学期望
的数学期望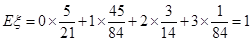 。
。
【解析】期望表示随机变量在随机试验中取值的平均值,它是概率意义下的平均值,不同于相应数值的算术平均数.解完此例题后归纳求离散型随机变量期望的步骤:①确定离散型随机变量 的取值.②写出分布列,并检查分布列的正确与否.③求出期望。
(1)由题意知本题是一个古典概型,试验发生包含的所有事件为从9个球中任取3个球有C93种结果,而满足条件取出的3个球颜色互不相同有C21C31C41种结果,根据古典概型公式得到结果.
(2)由题意知本题是一个古典概型,试验发生包含的所有事件为从9个球中任取3个球有C93种结果,而满足条件取出的3个球得分之和恰为1分有两种结果,包括取出1个红色球,2个白色球和取出2个红色球,1个黑色球,它们之间是互斥事件,
(3)ξ为取出的3个球中白色球的个数,由题意知ξ可能的取值为0,1,2,3.根据古典概型公式和试验包含的结果,得到白球个数不同是对应的概率,写出分布列,做出期望.
(Ⅰ)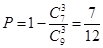 ………….. 3分
………….. 3分
(Ⅱ)记 “取出1个红色球,2个白色球”为事件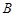 ,“取出2个红色球, 1个黑色球”为事件
,“取出2个红色球, 1个黑色球”为事件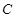 ,则
,则  .
………….. 6分
.
………….. 6分
(Ⅲ) 可能的取值为
可能的取值为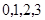 .………….. 7分
.………….. 7分
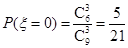 ,
,
 ,
,
 ,
,  .
………….. 11分
.
………….. 11分
 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
 的数学期望
的数学期望 . …12分
. …12分