题目内容
已知α是第三象限的角,sinα=-
,则
=( )
| 3 |
| 5 |
1-tan
| ||
1+tan
|
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |
分析:先根据α为第三象限角确定
的范围,进而利用万能公式利用sinα=-
求得tan
的值,然后代入所求的式子即可.
| α |
| 2 |
| 3 |
| 5 |
| α |
| 2 |
解答:解:∵α是第三象限角,
∴2kπ+π<α<2kπ+
∴kπ+
<
<kπ+
∴tan
<-1
sinα=
=-
整理得3tan2
+10tan
+3=0
求得tan
=-3或-
(排除)
则
=-2
故选D.
∴2kπ+π<α<2kπ+
| 3π |
| 2 |
∴kπ+
| π |
| 2 |
| α |
| 2 |
| 3π |
| 4 |
∴tan
| α |
| 2 |
sinα=
2tan
| ||
1+tan2
|
| 3 |
| 5 |
| α |
| 2 |
| α |
| 2 |
求得tan
| α |
| 2 |
| 1 |
| 3 |
则
1-tan
| ||
1+tan
|
故选D.
点评:本题主要考查了万能公式的化简求值,考查了学生对三角函数基本公式的掌握,特别要注意角的范围.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,
, 是第三象限的角,则
是第三象限的角,则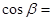 ________.
________. 且α是第三象限的角,则cos(α-2π)的值是 .
且α是第三象限的角,则cos(α-2π)的值是 . 且α是第三象限的角,则cos(2π-α)的值是( )
且α是第三象限的角,则cos(2π-α)的值是( )



 且α是第三象限的角,则cos(α-2π)的值是 .
且α是第三象限的角,则cos(α-2π)的值是 .