题目内容
(本小题满分12分)
已知定义域为 的函数
的函数 满足:①
满足:①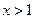 时,
时,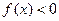 ;②
;② ③对任意的正实数
③对任意的正实数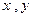 ,都有
,都有
(1)求证: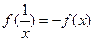 ;(2)求证:
;(2)求证: 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式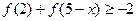 的解集.
的解集.
解: 因为对任意正实数x,y有f(x.y)=f(x)+f(y)
所以 f(1)=f(1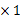 )=f(1)+f(1)=2f(1)
)=f(1)+f(1)=2f(1)
所以f(1)="0 " ----------------------------2分
(1)所以f( 1)=f(x
1)=f(x )=f(x)+f(
)=f(x)+f(
所以f(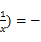 f(x) --
f(x) -- --------------------------------5分
--------------------------------5分
(2)设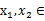 (0,+
(0,+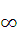 ),且
),且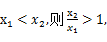 则f(
则f(
又由(1)知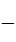 f(x)=f(
f(x)=f(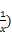
 f(
f(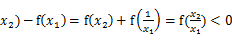
 f(
f( 为(0,
为(0,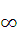 )的减函数----------8分
)的减函数----------8分
(3)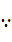 f
f (1)=f(2
(1)=f(2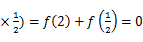 因为
因为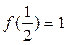
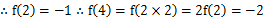
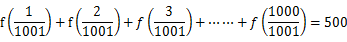
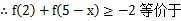
f(10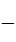 2x)
2x)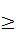 f(4)
f(4)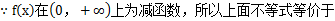
 得3
得3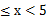 所以原不等式的解集为
所以原不等式的解集为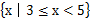 -------------------------12分
-------------------------12分
解析

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目