题目内容
已知双曲线的方程是16x2-9y2=144.(1)求这双曲线的焦点坐标、离心率和渐近线方程;
(2)设F1和F2是双曲线的左、右焦点,点P在双曲线上,且|PF1|•|PF2|=32,求∠F1PF2的大小.
【答案】分析:(1)向将双曲线转化为标准形式,得到a,b,c的值,即可得到焦点坐标、离心率和渐近线方程;
(2)先根据双曲线的定义得到||PF1|-|PF2||=6,再由余弦定理得到cos∠F1PF2的值,进而可得到∠F1PF2的大小.
解答:解:(1)由16x2-9y2=144得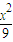 -
-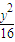 =1,
=1,
∴a=3,b=4,c=5.焦点坐标F1(-5,0),F2(5,0),离心率e= ,渐近线方程为y=±
,渐近线方程为y=± x.
x.
(2)||PF1|-|PF2||=6,
cos∠F1PF2=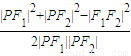
=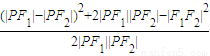 =
=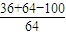 =0.
=0.
∴∠F1PF2=90°.
点评:本题主要考查双曲线的基本性质和余弦定理的应用,考查基础知识的简单应用.
(2)先根据双曲线的定义得到||PF1|-|PF2||=6,再由余弦定理得到cos∠F1PF2的值,进而可得到∠F1PF2的大小.
解答:解:(1)由16x2-9y2=144得
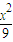 -
-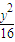 =1,
=1,∴a=3,b=4,c=5.焦点坐标F1(-5,0),F2(5,0),离心率e=
 ,渐近线方程为y=±
,渐近线方程为y=± x.
x.(2)||PF1|-|PF2||=6,
cos∠F1PF2=
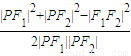
=
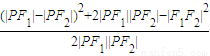 =
=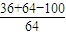 =0.
=0.∴∠F1PF2=90°.
点评:本题主要考查双曲线的基本性质和余弦定理的应用,考查基础知识的简单应用.

练习册系列答案
相关题目