题目内容
已知双曲线的方程是
-
=1,点P在双曲线上,且到其中一个焦点F1的距离为10,另一个焦点为F2,点N是PF1的中点,则ON的大小(O为坐标原点)为
| x2 |
| 16 |
| y2 |
| 8 |
1或9
1或9
.分析:连接ON,利用ON是三角形PF1F2的中位线,及双曲线的定义即可求得ON的大小.
解答: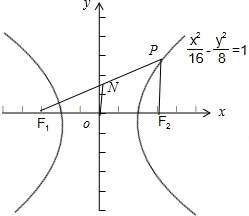 解:依题意,
解:依题意,
连接ON,ON是三角形PF1F2的中位线,所以ON=
PF2,
∵|PF1-PF2|=8,PF1=10,
∴PF2=2或18,
∴ON=
PF2=1或9.
故答案为:1或9.
 解:依题意,
解:依题意,连接ON,ON是三角形PF1F2的中位线,所以ON=
| 1 |
| 2 |
∵|PF1-PF2|=8,PF1=10,
∴PF2=2或18,
∴ON=
| 1 |
| 2 |
故答案为:1或9.
点评:本题考查双曲线的简单性质,考查三角形的中位线定理及双曲线的定义,考查分析与运算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
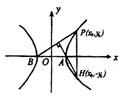 已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.
已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.