题目内容
椭圆M: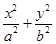 =1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆M上任一点,且
=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆M上任一点,且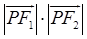 的最大值的取值范围是[2c2,3c2],其中
的最大值的取值范围是[2c2,3c2],其中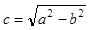 . 则椭圆M的离心率e的取值范围是( )
. 则椭圆M的离心率e的取值范围是( )
A.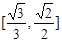 | B.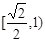 | C.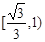 | D.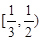 |
A
解析试题分析:因为 ,所以
,所以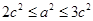 ,解得
,解得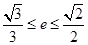 ,故选A.
,故选A.
或解设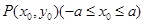 ,则
,则 ,
,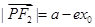 ,所以
,所以
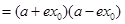
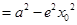 ,则
,则 的最大值为
的最大值为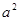 ,所以
,所以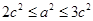 ,解得
,解得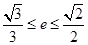 ,故选A.
,故选A.
考点:1.基本不等式的应用;2.离心率的求解.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知 ,且
,且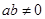 ,则下列结论恒成立的是 ( ).
,则下列结论恒成立的是 ( ).
A. | B.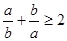 | C.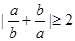 | D.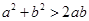 |
设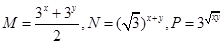 (
(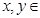 R
R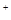 ,且
,且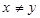 ), 则
), 则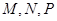 大小关系为( )
大小关系为( )
A.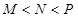 | B.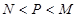 | C. | D. |
设椭圆 +
+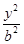 =1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为( )
=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为( )
A. ab ab | B. ab ab | C. ab ab | D.2ab |
函数y=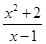 (x>1)的最小值是( )
(x>1)的最小值是( )
A.2 +2 +2 | B.2 -2 -2 | C.2 | D.2 |
下列函数中,最小值为4的是 ( )
A. | B. |
C. | D.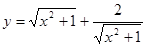 |
若 ,则
,则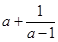 的最小值是( )
的最小值是( )
A.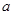 | B.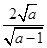 | C.2 | D.3 |
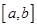 的函数
的函数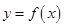 的图象的两个端点为
的图象的两个端点为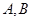 ,
, 是
是 图象上任意一点,其中
图象上任意一点,其中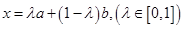 ,向量
,向量 ,若不等式
,若不等式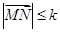 恒成立,则称函数
恒成立,则称函数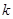 阶线性近似”. 若函数
阶线性近似”. 若函数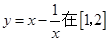 上“
上“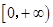
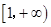
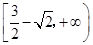
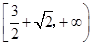
 是
是 内一点,且
内一点,且 的面积为2,定义
的面积为2,定义 ,其中
,其中 分别是ΔMBC,ΔMCA,ΔMAB的面积,若
分别是ΔMBC,ΔMCA,ΔMAB的面积,若 满足
满足 ,则
,则 的最小值是( )
的最小值是( )