题目内容
已知a、b∈R，下列四个式子中，甲是乙的必要非充分条件是（ ）
①甲：（a-1）（a+2）=0，乙：a=-2；
②甲：a，b不都为偶数，乙：a+b不为偶数
③甲：b2=ac，乙：
=
；
④甲：a＞6，乙：a＞2．
①甲：（a-1）（a+2）=0，乙：a=-2；
②甲：a，b不都为偶数，乙：a+b不为偶数
③甲：b2=ac，乙：
| a |
| b |
| b |
| c |
④甲：a＞6，乙：a＞2．
分析：必要条件说明甲可以被乙推出，非充分条件说明由甲不能推出乙成立．由此可以对四个情况逐个加以试验，证明其必要性成立充分性不成立，或举反例说明书有充分性而没有必要性，这样就可以选出正确的答案．
解答：解：对各个选项逐个加以判别：
对于①，甲：（a-1）（a+2）=0，说明a=-2或a=1，乙不一定成立，
但反之一定成立，故是必要非充分条件；
再看②，甲：a，b不都为偶数，说明a+b为偶数或为奇数，
乙不一定成立，但反之一定成立，故是必要非充分条件；
再看③甲：b2=ac，有可能三个数均为0，那么乙：
=
就不一定成立了，
而反之由乙：
=
一定得到甲b2=ac，也是必要非充分条件；
④甲：a＞6一定可以推出乙：a＞2成立，是充分条件，说明甲不是乙的必要非充分条件．
正确选项是①②③
故选A
对于①，甲：（a-1）（a+2）=0，说明a=-2或a=1，乙不一定成立，
但反之一定成立，故是必要非充分条件；
再看②，甲：a，b不都为偶数，说明a+b为偶数或为奇数，
乙不一定成立，但反之一定成立，故是必要非充分条件；
再看③甲：b2=ac，有可能三个数均为0，那么乙：
| a |
| b |
| b |
| c |
而反之由乙：
| a |
| b |
| b |
| c |
④甲：a＞6一定可以推出乙：a＞2成立，是充分条件，说明甲不是乙的必要非充分条件．
正确选项是①②③
故选A
点评：本题考查了充要条件的判断，属于基础题．充分条件是推出其它条件的条件，而必要条件是被其它条件推出的条件，再在此基础上加以证明或举出反例，则不难得出问题的答案．
练习册系列答案
相关题目
B．a2＋b2≥2ab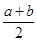
)2 D．|a|＋|b|≥2