题目内容
【题目】等差数列{an}中，a3+a4=4，a5+a7=6．
（1）求{an}的通项公式；
（2）设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．
【答案】
（1）
解：设等差数列{an}的公差为d，
∵a3+a4=4，a5+a7=6．
∴ 
，
解得：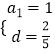 
，
∴an= 
；
（2）
解：∵bn=[an]，
∴b1=b2=b3=1，
b4=b5=2，
b6=b7=b8=3，
b9=b10=4．
故数列{bn}的前10项和S10=3×1+2×2+3×3+2×4=24
【解析】（Ⅰ）设等差数列{an}的公差为d，根据已知构造关于首项和公差方程组，解得答案（2）根据bn=[an]，列出数列{bn}的前10项，相加可得答案．；本题考查的知识点是等差数列的通项公式，等差数列的性质，难度中档．
【考点精析】本题主要考查了等差数列的通项公式（及其变式）和等差数列的性质的相关知识点，需要掌握通项公式：
或
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列才能正确解答此题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
