题目内容
 (2011•通州区一模)已知椭圆C:
(2011•通州区一模)已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(I)求椭圆C的方程;
(II)求经过点A(4,0)且与椭圆C相切的直线方程;
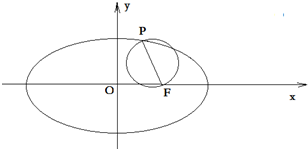
(III)设P为椭圆C上一动点,以PF为直径的动圆内切于一个定圆E.求定圆E的方程.
分析:(I)利用椭圆的离心率为e=
,右焦点为F(1,0),求出a,c,利用b2=a2-c2,可求b的值,从而可求椭圆C的方程;
(II)设出经过点A(4,0)且与椭圆C相切的直线方程,代入椭圆方程,利用判别式为0,即可得到结论;
(III)利用椭圆的定义,可得以PF为直径的圆与以椭圆长轴为直径的圆内切,从而可得结论.
| 1 |
| 2 |
(II)设出经过点A(4,0)且与椭圆C相切的直线方程,代入椭圆方程,利用判别式为0,即可得到结论;
(III)利用椭圆的定义,可得以PF为直径的圆与以椭圆长轴为直径的圆内切,从而可得结论.
解答:解:(I)∵椭圆的离心率为e=
,右焦点为F(1,0).
∴
=
,c=1
∴a=2,b2=a2-c2=3
∴椭圆C的方程为
+
=1;
(II)设经过点A(4,0)且与椭圆C相切的直线方程为y=k(x-4)
代入椭圆方程可得(3+4k2)x2-32k2x+64k2-12=0
∴△=(32k2)-4(3+4k2)(64k2-12)=0
∴k2=
∴k=±
∴所求直线方程为y=±
(x-4);
(III)利用椭圆的定义,可得以PF为直径的圆与以椭圆长轴为直径的圆内切
设PF的中点为C,则OC=
=2-
∴以PF为直径的动圆内切于一个定圆E,圆心为(0,0),半径为半长轴长
∴定圆E的方程的方程为x2+y2=4.
| 1 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
∴a=2,b2=a2-c2=3
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)设经过点A(4,0)且与椭圆C相切的直线方程为y=k(x-4)
代入椭圆方程可得(3+4k2)x2-32k2x+64k2-12=0
∴△=(32k2)-4(3+4k2)(64k2-12)=0
∴k2=
| 1 |
| 4 |
∴k=±
| 1 |
| 2 |
∴所求直线方程为y=±
| 1 |
| 2 |
(III)利用椭圆的定义,可得以PF为直径的圆与以椭圆长轴为直径的圆内切
设PF的中点为C,则OC=
| 4-PF |
| 2 |
| PF |
| 2 |
∴以PF为直径的动圆内切于一个定圆E,圆心为(0,0),半径为半长轴长
∴定圆E的方程的方程为x2+y2=4.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查圆与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (2011•通州区一模)在长方体ABCD-A1B1C1D1中,用过A,B1,D1三点的平面将其一角A1AB1D1截下,所得到的几何体ABCD-B1C1D1的左视图是( )
(2011•通州区一模)在长方体ABCD-A1B1C1D1中,用过A,B1,D1三点的平面将其一角A1AB1D1截下,所得到的几何体ABCD-B1C1D1的左视图是( )