Question

5．已知m∈R，函数f（x）=mx²-lnx
（1）不等式f（x）≥x恒成立，求m的最小值；
（2）当m=$\frac{1}{2}$时，证明方程f（x）=x有两个不等的实根；
（3）当m=1时，关于x的方程f（x）=kx有两个不等的实根，求实数k的取值范围．

Answer 1

分析 （1）先求出函数的定义域，问题转化为m≥$\frac{x+lnx}{{x}^{2}}$恒成立即可；
（2）将m的值代入函数f（x）的表达式，问题转化为函数m（x）=$\frac{1}{2}$x²-x和函数n（x）=lnx有两个不同的交点，画出图象读出即可；
（3）将m=1的值代入f（x），问题转化为p（x）=x²-kx和q（x）=lnx有2个不同的交点，通过画出函数的草图，判断k的范围即可．

解答 解：函数f（x）的定义域是（0，+∞），
（1）不等式f（x）≥x恒成立，
即：m≥$\frac{x+lnx}{{x}^{2}}$恒成立，
令g（x）=$\frac{x+lnx}{{x}^{2}}$，（x＞0），
则g′（x）=$\frac{1-x-2lnx}{{x}^{3}}$，
由g′（x）＞0，解得：0＜x＜1，
由g′（x）＜0，解得：x＞1，
∴g（x）在（0，1）递增，在（1，+∞）递减，
∴g（x）_max=g（1）=1，
∴m≥1，m的最小值是1；
（2）m=$\frac{1}{2}$时：f（x）=$\frac{1}{2}$x²-lnx，
若证明方程f（x）=x有两个不等的实根，
即证明函数m（x）=$\frac{1}{2}$x²-x和函数n（x）=lnx有两个不同的交点，
画出函数m（x），n（x）的图象，如图示：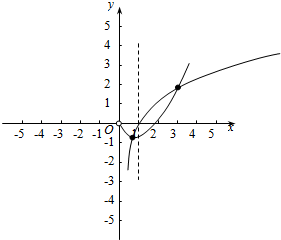
，
∴方程f（x）=x有两个不等的实根；
（3）m=1时：f（x）=x²-lnx，
若关于x的方程f（x）=kx有两个不等的实根，
则x²-kx=lnx有2个不相等的实数根，
即p（x）=x²-kx和q（x）=lnx有2个不同的交点，
而p（x）的对称轴是：x=$\frac{k}{2}$，只需$\frac{k}{2}$＞0即k＞0即可．

点评 不同考查了二次函数的性质，考查函数恒成立问题，考查数形结合思想，转化思想，是一道中档题．