题目内容
设等比数列{an}的首项为a1=2,公比为q(q为正整数),且满足3a3是8a1与a5的等差中项;数列{an}满足2n2-(t+bn)n+ bn=0(t∈R,n∈N*).
bn=0(t∈R,n∈N*).
(1)求数列{an}的通项公式;
(2)试确定实数t的值,使得数列{bn}为等差数列.
解:(1)由题意,6a3=8a1+a5,则6q2=8+q4,解得q2=4或q2=2,
因为q为正整数,所以q=2,又a1=2,所以an=2n
(2)当n=1时,2-(t+b1)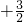 b1=0,得b1=2t-4,
b1=0,得b1=2t-4,
同理可得:n=2时,b2=16-4t,n=3时,b3=12-2t,
则由b1+b3=2b2,得t=3,
并且,当t=3时,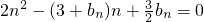 ,
,
得bn=2n,由bn+1-bn=2,知此时数列{bn}为等差数列.
故答案为:t=3.
分析:(1)由题意,6a3=8a1+a5,则6q2=8+q4,解得q2=4或q2=2,因为q为正整数,所以q=2,故可得通项;
(2)分别令n=1,2,3,可得得b1=2t-4,b2=16-4t,b3=12-2t,由b1+b3=2b2,可得得t=3,代入原式可得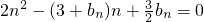 ,得bn=2n,由等差数列的定义可判.
,得bn=2n,由等差数列的定义可判.
点评:本题为等差、等比数列的综合应用,正确运用公式是解决问题的关键,属基础题.
因为q为正整数,所以q=2,又a1=2,所以an=2n
(2)当n=1时,2-(t+b1)
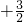 b1=0,得b1=2t-4,
b1=0,得b1=2t-4,同理可得:n=2时,b2=16-4t,n=3时,b3=12-2t,
则由b1+b3=2b2,得t=3,
并且,当t=3时,
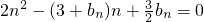 ,
,得bn=2n,由bn+1-bn=2,知此时数列{bn}为等差数列.
故答案为:t=3.
分析:(1)由题意,6a3=8a1+a5,则6q2=8+q4,解得q2=4或q2=2,因为q为正整数,所以q=2,故可得通项;
(2)分别令n=1,2,3,可得得b1=2t-4,b2=16-4t,b3=12-2t,由b1+b3=2b2,可得得t=3,代入原式可得
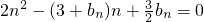 ,得bn=2n,由等差数列的定义可判.
,得bn=2n,由等差数列的定义可判.点评:本题为等差、等比数列的综合应用,正确运用公式是解决问题的关键,属基础题.

练习册系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |