题目内容
已知向量满足| |=2|
|=2| |,若p:关于x的方程x2+|
|,若p:关于x的方程x2+| |x+
|x+ •
• =0没有实数根;q:向量
=0没有实数根;q:向量 ,
, 的夹角θ∈[0,
的夹角θ∈[0, ),则p是q的( )
),则p是q的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:因为方程x2+|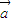 |x+
|x+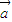 •
•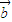 =0没有实数根,所以
=0没有实数根,所以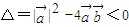 .因为|
.因为|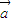 |=2|
|=2|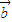 |,所以cosθ>
|,所以cosθ> .因为θ∈[0,π],所以θ∈[0,
.因为θ∈[0,π],所以θ∈[0,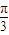 ].所以p:向量
].所以p:向量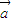 ,
,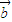 的夹角θ∈[0,
的夹角θ∈[0,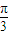 ),所以q⇒p.
),所以q⇒p.
解答:解:因为方程x2+|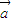 |x+
|x+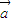 •
•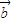 =0没有实数根,
=0没有实数根,
所以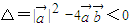
即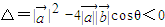
因为|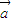 |=2|
|=2|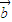 |,
|,
所以cosθ>
因为θ∈[0,π]
所以θ∈[0,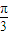 ].
].
所以p:向量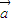 ,
,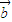 的夹角θ∈[0,
的夹角θ∈[0,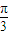 )
)
又因为q:向量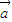 ,
,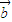 的夹角θ∈[0,
的夹角θ∈[0,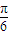 ),
),
所以q⇒p
所以p是q的必要不充分条件.
故选B.
点评:解决此类问题的方法是当出现较为复杂的充要条件判断问题时,可以先求其充要条件,然后转化为两个简单条件的关系判断,也可以转化为两个集合之间的关系进行判断.
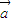 |x+
|x+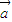 •
•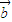 =0没有实数根,所以
=0没有实数根,所以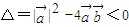 .因为|
.因为|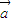 |=2|
|=2|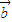 |,所以cosθ>
|,所以cosθ> .因为θ∈[0,π],所以θ∈[0,
.因为θ∈[0,π],所以θ∈[0,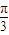 ].所以p:向量
].所以p:向量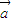 ,
,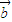 的夹角θ∈[0,
的夹角θ∈[0,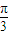 ),所以q⇒p.
),所以q⇒p.解答:解:因为方程x2+|
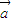 |x+
|x+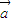 •
•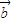 =0没有实数根,
=0没有实数根,所以
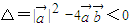
即
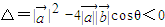
因为|
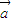 |=2|
|=2|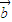 |,
|,所以cosθ>

因为θ∈[0,π]
所以θ∈[0,
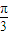 ].
].所以p:向量
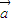 ,
,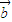 的夹角θ∈[0,
的夹角θ∈[0,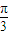 )
)又因为q:向量
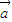 ,
,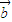 的夹角θ∈[0,
的夹角θ∈[0,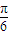 ),
),所以q⇒p
所以p是q的必要不充分条件.
故选B.
点评:解决此类问题的方法是当出现较为复杂的充要条件判断问题时,可以先求其充要条件,然后转化为两个简单条件的关系判断,也可以转化为两个集合之间的关系进行判断.

练习册系列答案
相关题目
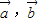 满足|
满足|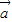 |=2,|
|=2,|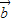 |=1,
|=1,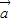 与
与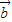 的夹角为60°,则|
的夹角为60°,则|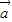 -2
-2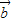 |等于 .
|等于 .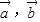 满足|
满足|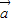 |=2,|
|=2,|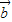 |=1,
|=1,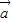 与
与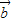 的夹角为60°,则|
的夹角为60°,则|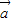 -2
-2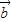 |等于 .
|等于 .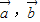 满足|
满足|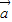 |=2,|
|=2,|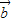 |=1,
|=1,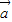 与
与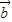 的夹角为60°,则|
的夹角为60°,则|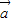 -2
-2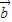 |等于 .
|等于 .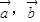 满足|
满足|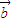 |=2,
|=2,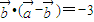 ,则向量
,则向量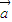 在
在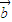 上的投影为 .
上的投影为 .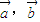 满足|
满足|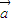 |=2,|
|=2,|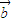 |=1,
|=1,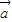 与
与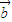 的夹角为60°,则|
的夹角为60°,则|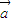 -2
-2 |等于 .
|等于 .