题目内容
已知向量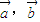 满足|
满足|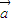 |=2,|
|=2,|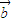 |=1,
|=1,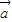 与
与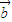 的夹角为60°,则|
的夹角为60°,则|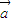 -2
-2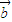 |等于 .
|等于 .
【答案】分析:先将所求向量的模平方,转化为向量数量积运算,再利用已知两向量的模和夹角,利用数量积运算性质计算即可,最后别忘了开平方
解答:解:∵| |=2,|
|=2,| |=1,
|=1, 与
与 的夹角为60°
的夹角为60°
∴| |2=
|2= -4
-4 +4
+4
=4-4×2×1×cos60°+4×1
=4-4+4=4
∴| |=2
|=2
故答案为2
点评:本题主要考查了单位向量、向量夹角的概念,向量数量积运算及其性质的应用,求向量的模的一般方法
解答:解:∵|
 |=2,|
|=2,| |=1,
|=1, 与
与 的夹角为60°
的夹角为60°∴|
 |2=
|2= -4
-4 +4
+4
=4-4×2×1×cos60°+4×1
=4-4+4=4
∴|
 |=2
|=2故答案为2
点评:本题主要考查了单位向量、向量夹角的概念,向量数量积运算及其性质的应用,求向量的模的一般方法

练习册系列答案
相关题目
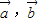 满足|
满足|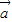 |=2,|
|=2,|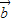 |=1,
|=1,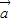 与
与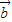 的夹角为60°,则|
的夹角为60°,则|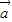 -2
-2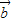 |等于 .
|等于 .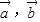 满足|
满足|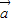 |=2,|
|=2,|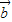 |=1,
|=1,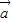 与
与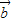 的夹角为60°,则|
的夹角为60°,则|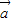 -2
-2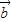 |等于 .
|等于 .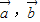 满足|
满足|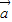 |=2,|
|=2,|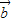 |=1,
|=1,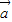 与
与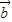 的夹角为60°,则|
的夹角为60°,则|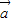 -2
-2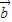 |等于 .
|等于 .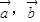 满足|
满足|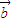 |=2,
|=2,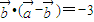 ,则向量
,则向量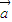 在
在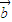 上的投影为 .
上的投影为 .