题目内容
15．定义在（-8，8）上的函数f（x）既为减函数，又为奇函数，解关于a的不等式f（7-a）+f（5-a）＜0．分析 根据函数的奇偶性可将原不等式化为f（7-a）＜f（a-5），再结合函数的单调性和定义域，可得-8＜a-5＜7-a＜8，解得答案．
解答 解：∵f（x）的定义坸为（-8，8），且函数f（x）既为减函数，又为奇函数，
∴不等式f（7-a）+f（5-a）＜0，
可化为：f（7-a）＜-f（5-a）=f（a-5），
即-8＜a-5＜7-a＜8，
解得：a∈（-1，6）
点评 本题考查的知识点是函数奇偶性和单调性的综合应用，是函数图象和性质的简单综合．
练习册系列答案
相关题目
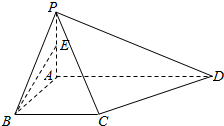如图，在四棱锥P-ABCD中，∠DAB=∠ABC=90°，PA⊥平面ABCD，点E是PA的中点，AB=BC=1，AD=2．求证：
已知正四棱锥S-ABCD的底面边长为a，侧棱长为2a，点P，Q分别在BD和SC上，并且BP：PD=1：3，PQ∥平面SAD，求线段PQ的长．