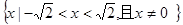题目内容
不等式 对于
对于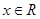 恒成立,那么
恒成立,那么 的取值范围是( )
的取值范围是( )
A. | B.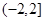 | C. | D. |
B
解析试题分析:因为要使得不等式 对于
对于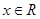 恒成立,那么要考虑当a-2=0时,即a=2,原不等式等价于-4<0显然恒成立,当a
恒成立,那么要考虑当a-2=0时,即a=2,原不等式等价于-4<0显然恒成立,当a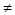 2时,则根据二次函数性质可知,只有开口向下,判别式小于零时满足题意,即
2时,则根据二次函数性质可知,只有开口向下,判别式小于零时满足题意,即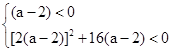 ,解得-2<a<2,综上可知参数a的范围是
,解得-2<a<2,综上可知参数a的范围是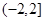 ,故选B.
,故选B.
考点:本试题主要考查了含有参数的一元二次不等式的恒成立问题的运用。
点评:解决该试题的关键是要对参数a-2是否为零进行分类讨论,确定出不等式的性质,分别验证并求解得到结论。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设 ,
, ,
, ,则它们的大小关系是
,则它们的大小关系是
A. | B. | C. | D.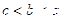 |
在R上定义运算 若不等式
若不等式 对任意实数
对任意实数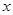 成立,则( )
成立,则( )
A. | B.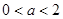 |
C.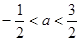 | D.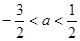 |
关于 的不等式
的不等式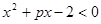 的解集是
的解集是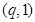 ,则
,则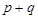 的值为( )
的值为( )
A. | B.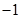 | C.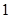 | D.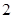 |
设不等式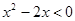 的解集为M,函数
的解集为M,函数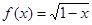 的定义域为N,则
的定义域为N,则 为( )
为( )
| A.(0,1) | B.(0,2) | C.(0,1] | D.(0,2] |
(理)在R上定义运算 :x
:x y=x(1-y),若不等式(x-a)
y=x(1-y),若不等式(x-a) (x+a)<1对任意实数x都成立,则
(x+a)<1对任意实数x都成立,则
A.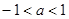 | B.0<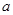 <2 <2 | C. | D.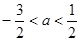 |
不等式 对任意实数
对任意实数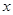 恒成立,则实数
恒成立,则实数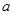 的取值范围为( )
的取值范围为( )
A. | B.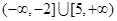 |
C. | D.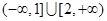 |
不等式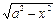 <2x+a(a>0)的解集是 ( )
<2x+a(a>0)的解集是 ( )
A.{x|-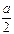 <x<a <x<a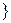 | B.{x|x>0或x<-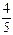 a a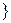 |
C.{x|-a≤x<-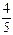 a或0≤x<a a或0≤x<a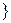 | D.{x|0<x≤a= |
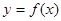 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在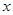 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式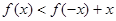 的解集为 ( )
的解集为 ( )