题目内容
(理)在R上定义运算 :x
:x y=x(1-y),若不等式(x-a)
y=x(1-y),若不等式(x-a) (x+a)<1对任意实数x都成立,则
(x+a)<1对任意实数x都成立,则
A.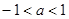 | B.0<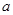 <2 <2 | C. | D.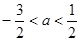 |
C
解析试题分析:由题意知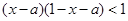 恒成立,即
恒成立,即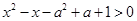 恒成立,所以
恒成立,所以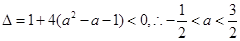 .
.
考点:一元二次不等式恒成立.
点评:本小题关键是搞请楚新运算:x y=x(1-y),从而把不等式(x-a)
y=x(1-y),从而把不等式(x-a) (x+a)<1转化为
(x+a)<1转化为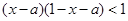 恒成立问题来解决.
恒成立问题来解决.

练习册系列答案
相关题目
若方程 在(0,1)内恰有一解,则a的取值范围是( )
在(0,1)内恰有一解,则a的取值范围是( )
A. | B.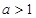 | C. | D. |
设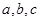 均为正数,且
均为正数,且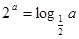 ,
,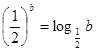 ,
,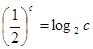 则( )
则( )
A. | B.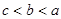 | C.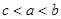 | D.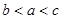 |
不等式 对于
对于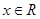 恒成立,那么
恒成立,那么 的取值范围是( )
的取值范围是( )
A. | B.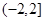 | C. | D. |
不等式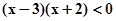 的解集为( )
的解集为( )
A.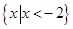 | B. | C.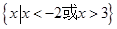 | D.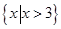 |
不等式-6x2-x+2≤0的解集是( )
A. | B. |
C. | D. |
不等式(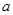 -2)
-2)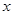 2+2(
2+2(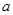 -2)
-2)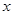 -4<0,对一切
-4<0,对一切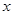 ∈R恒成立,则a的取值范围是( )
∈R恒成立,则a的取值范围是( )
| A.(-∞,2] | B.(-2,2] | C.(-2,2) | D.(-∞,2) |
 ,则a+b= _____________.
,则a+b= _____________. 的解集为( )
的解集为( )






