题目内容
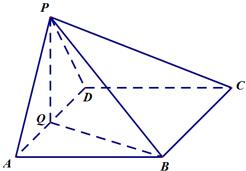 如图:四边形ABCD是边长为2的菱形,∠BAD=60°,点P是平面ABCD外一点,且PB=2,在等腰直角三角形PAD中,Q是斜边AD的中点.
如图:四边形ABCD是边长为2的菱形,∠BAD=60°,点P是平面ABCD外一点,且PB=2,在等腰直角三角形PAD中,Q是斜边AD的中点.(1)求证:PQ⊥平面ABCD;
(2)求二面角Q-PB-D的大小;
(3)点M在线段PC上,PM=tPC,试确定实数t的值,使得PA∥平面MQB.
分析:(1)由已知中四边形ABCD是边长为2的菱形,∠BAD=60°,等腰直角三角形PAD中,Q是斜边AD的中点,由求出PB,QB,PQ值,由勾股定理可得PQ⊥QB,又由PQ⊥AD,由线面垂直的判定定理可得PQ⊥平面ABCD;
(2)建立空间直角坐标系Q-xyz,求出平面PBD的法向量,及平面PQB的法向量,代入向量夹角公式,可得答案.
(3)连接AC,交QB于O点,连接OM,BM,QM,由线面平行的判定定理可得则需使PA∥OM,由PM=tPC,由平行线分线段成比例定理可得AO=tAC,由底面四边形ABCD是边长为2的菱形,∠BAD=60°可得答案.
(2)建立空间直角坐标系Q-xyz,求出平面PBD的法向量,及平面PQB的法向量,代入向量夹角公式,可得答案.
(3)连接AC,交QB于O点,连接OM,BM,QM,由线面平行的判定定理可得则需使PA∥OM,由PM=tPC,由平行线分线段成比例定理可得AO=tAC,由底面四边形ABCD是边长为2的菱形,∠BAD=60°可得答案.
解答:证明:(1)∵四边形ABCD是边长为2的菱形,∠BAD=60°,PB=2,
∴QB=
又∵三角形PAD为等腰直角三角
∴PQ=1
⇒PQ2+QB2=PB2⇒PQ⊥QB,
又PQ⊥AD,AD∩QB=Q
故PQ⊥平面ABCD…(3分)
(2)∵四边形ABCD是菱形,∠BAD=60°
∴BQ⊥AD如图所示,建立空间直角坐标系Q-xyz
则B(0,
,0),D(-1,0,0),P(0,0,1),Q(0,0,0)
则
=(0,
,-1),
=(-1,0,-1)
设
=(x,y,z)是平面PBD的法向量,
则
•
=0,
•
=0,
即
令y=1,则
=(-
,1,
)
又∵x轴⊥平面PQB
∴
=(1,0,0)是平面PQB的法向量,
∴cos<
,
>=
=
=-
∵二面角Q-PB-D是锐角
∴二面角Q-PB-D的大小为arccos
…(6分)
(3)连接AC,交QB于O点,连接OM,BM,QM
若使得PA∥平面MQB
则需使PA∥OM
∵PM=tPC
∴AO=tAC
在菱形ABCD中,
可得t=
….(10分)
∴QB=
| 3 |
又∵三角形PAD为等腰直角三角
∴PQ=1
|
又PQ⊥AD,AD∩QB=Q
故PQ⊥平面ABCD…(3分)
(2)∵四边形ABCD是菱形,∠BAD=60°
∴BQ⊥AD如图所示,建立空间直角坐标系Q-xyz
则B(0,
| 3 |
则
| PB |
| 3 |
| PD |
设
| n |

则
| n |
| PB |
| n |
| PD |
即
|
令y=1,则
| n |
| 3 |
| 3 |
又∵x轴⊥平面PQB
∴
| m |
∴cos<
| m |
| n |
| ||||
|
|
-
| ||
|
| ||
| 7 |
∵二面角Q-PB-D是锐角
∴二面角Q-PB-D的大小为arccos
| ||
| 7 |
(3)连接AC,交QB于O点,连接OM,BM,QM
若使得PA∥平面MQB
则需使PA∥OM
∵PM=tPC
∴AO=tAC
在菱形ABCD中,
可得t=
| 1 |
| 3 |
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,其中熟练掌握空间线面关系的判定定理,及向量法解二面角问题的方法和步骤,是解答本题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=