题目内容
((本小题满分14分)
已知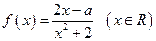 。
。
(1)若函数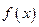 为奇函数,求实数
为奇函数,求实数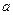 的值;
的值;
(2)若函数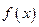 在区间
在区间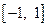 上是增函数,求实数
上是增函数,求实数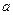 的值组成的集合A;
的值组成的集合A;
(3)设关于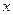 的方程
的方程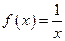 的两个非零实根为
的两个非零实根为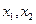 ,试问:是否存在实数
,试问:是否存在实数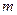 ,使得不等式
,使得不等式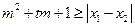 对任意
对任意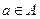 及
及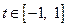 恒成立?若存在,求
恒成立?若存在,求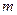 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
已知
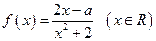 。
。 (1)若函数
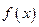 为奇函数,求实数
为奇函数,求实数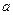 的值;
的值;(2)若函数
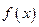 在区间
在区间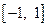 上是增函数,求实数
上是增函数,求实数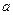 的值组成的集合A;
的值组成的集合A;(3)设关于
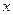 的方程
的方程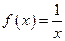 的两个非零实根为
的两个非零实根为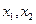 ,试问:是否存在实数
,试问:是否存在实数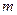 ,使得不等式
,使得不等式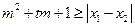 对任意
对任意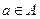 及
及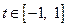 恒成立?若存在,求
恒成立?若存在,求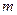 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。解:(1)根据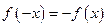 恒成立得到
恒成立得到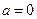
(2)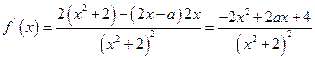
根据题意知,在区间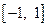 恒有
恒有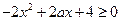 ,故有
,故有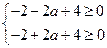
解之得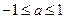 ,即
,即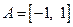
(3)由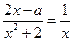 得
得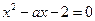 ,所以
,所以
故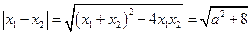 ,因为
,因为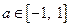 ,故
,故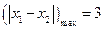
所以只需要对于任意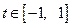 ,
,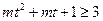 恒成立。
恒成立。
令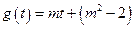 ,则有
,则有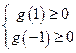 ,即
,即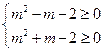
解得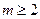 或
或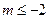
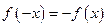 恒成立得到
恒成立得到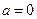
(2)
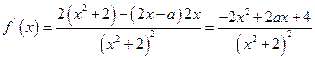
根据题意知,在区间
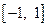 恒有
恒有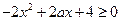 ,故有
,故有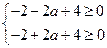
解之得
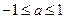 ,即
,即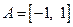
(3)由
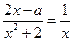 得
得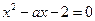 ,所以
,所以
故
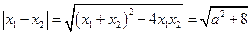 ,因为
,因为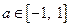 ,故
,故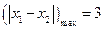
所以只需要对于任意
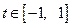 ,
,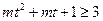 恒成立。
恒成立。令
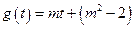 ,则有
,则有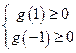 ,即
,即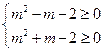
解得
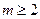 或
或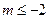
略

练习册系列答案
相关题目
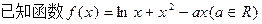
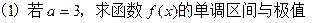

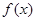 的定义域为
的定义域为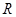 ,对任意的
,对任意的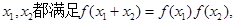
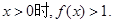
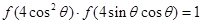 ,求
,求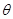 的值;
的值;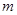 ,当
,当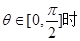 ,使不等式
,使不等式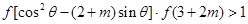 对所有的
对所有的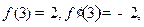 则
则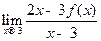 的值为 ( )
的值为 ( ) 
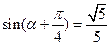 ,则
,则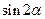 等于 ( )
等于 ( ) 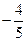
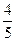
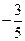

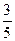
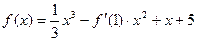 ,则
,则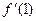 =" "
=" " 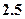 元,销售价是每束
元,销售价是每束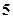 元;节后卖不出的鲜花以每束
元;节后卖不出的鲜花以每束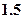
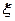
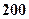
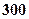
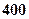
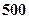
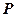
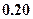
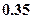
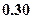
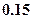
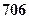 元
元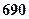 元
元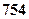 元
元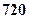 元
元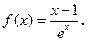
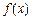 的单调区间和极值;
的单调区间和极值;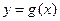 对任意
对任意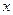 满足
满足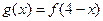 ,求证:当
,求证:当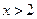 ,
,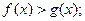
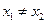 ,且
,且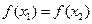 ,求证:
,求证: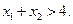
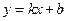 与曲线
与曲线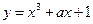 相切于点(2,3),则b的值为 。
相切于点(2,3),则b的值为 。