题目内容
右图是一几何体的平面展开图，其中四边形ABCD为正方形，E、F分别为PA、PD的中点，在此几何体中，给出下面四个结论：
①直线BE与直线CF是异面直线；②直线BE与直线AF是异面直线；
③直线EF∥平面PBC；④平面BCE⊥平面PAD.
其中正确结论的序号是( )
A．①② B．②③ C．①④ D．②④
B
解析
练习册系列答案
相关题目
若m、n为两条不同的直线，α、β为两个不同的平面，则以下命题正确的是( )．
| A．若m∥α，n∥α，则m∥n | B．若m∥n，m⊥α，则n⊥α |
| C．若m∥β，α∥β，则m∥α | D．若α∩β＝m，m⊥n，则n⊥α |
在正方体
中，E是棱
的中点，则BE与平面
所成角的正弦值为
A． | B． | C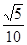． | D． |
空间四边形ABCD中，若
，则
与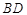
所成角为( )
A． | B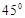． | C． | D． |
空间四边形ABCD中, AC="AD," BC="BD," 则AB与CD所成的角为
| A．300 | B．450 | C．600 | D．900 |
设m，n为两条直线，α，β为两个平面，则下列四个命题中，正确的命题是( )
| A．若m?α，n?α，且m∥β，n∥β，则α∥β |
| B．若m∥α，m∥n，则n∥α |
| C．若m∥α，n∥α，则m∥n |
| D．若m，n为两条异面直线，且m∥α，n∥α，m∥β，n∥β，则α∥β |
若一个二面角的两个半平面与另一个二面角的两个半平面互相垂直，则这两个二面角的大小 ( )
| A．相等 | B．互补 | C．相等或互补 | D．无法确定 |
，PA⊥平面ABC，则四面体P-ABC中共有（ ）个直角三角形