题目内容
现有一组互不相同且从小到大排列的数据a,a1,a2,a3,a4,a5,其中a=0.记T=a+a1+a2+a3+a4+a5,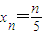 ,
,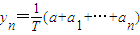 (n=0,1,2,3,4,5),作函数y=f(x),使其图象为逐点依次连接点Pn(xn,yn)(n=0,1,2,3,4,5)的折线.
(n=0,1,2,3,4,5),作函数y=f(x),使其图象为逐点依次连接点Pn(xn,yn)(n=0,1,2,3,4,5)的折线.(Ⅰ)求f(0)和f(1)的值;
(Ⅱ)设直线Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1,k2,k3,k4,k5的大小关系;
(Ⅲ)证明:当x∈(0,1)时,f(x)<x.
【答案】分析:(Ⅰ)结合已知代入可求f(0)=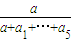 ,f(1)=
,f(1)=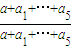 即可求解
即可求解
(Ⅱ)由题意可得,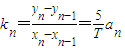 ,结合已知a<a1<a2<a3<a4<a5,可判断
,结合已知a<a1<a2<a3<a4<a5,可判断
(Ⅲ)要证明f(x)<x(0<x<1),只需证明f(xn)<xn,
法一:可证5(a1+a2+…+an)=[n+(5-n)](a1+a2+…+an)<nT,即可证明
法二:kn<1时,yn=(y1-y)+(y2-y1)+…+(yn-yn-1)
当kn≥1时,yn=y5-(y5-yn)=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]可证明
解答:(Ⅰ)解: ,…(2分)
,…(2分)
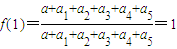 ; …(4分)
; …(4分)
(Ⅱ)解: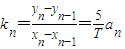 ,n=1,2,3,4,5. …(6分)
,n=1,2,3,4,5. …(6分)
因为 a<a1<a2<a3<a4<a5,
所以 k1<k2<k3<k4<k5. …(8分)
(Ⅲ)证:由于f(x)的图象是连接各点Pn(xn,yn)(n=0,1,2,3,4,5)的折线,
要证明f(x)<x(0<x<1),只需证明f(xn)<xn(n=1,2,3,4).…(9分)
事实上,当x∈(xn-1,xn)时,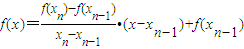 =
=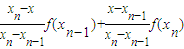
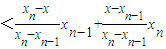 =x.
=x.
下面证明f(xn)<xn.
法一:对任何n(n=1,2,3,4),5(a1+a2+…+an)=[n+(5-n)](a1+a2+…+an)…(10分)=n(a1+a2+…+an)+(5-n)(a1+a2+…+an)≤n(a1+a2+…+an)+(5-n)nan…(11分)=n[a1+a2+…+an+(5-n)an]<n(a1+a2+…+an+an+1+…+a5)=nT…(12分)
所以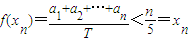 .…(13分)
.…(13分)
法二:对任何n(n=1,2,3,4),
当kn<1时,yn=(y1-y)+(y2-y1)+…+(yn-yn-1)=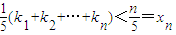 ;…(10分)
;…(10分)
当kn≥1时,yn=y5-(y5-yn)=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]=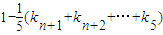
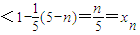 .
.
综上,f(xn)<xn. …(13分)
点评:本题以新定义为载体,主要考查了数列的求和及一定的推理与运算的能力,试题具有一定的综合性
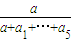 ,f(1)=
,f(1)=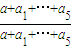 即可求解
即可求解(Ⅱ)由题意可得,
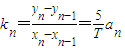 ,结合已知a<a1<a2<a3<a4<a5,可判断
,结合已知a<a1<a2<a3<a4<a5,可判断(Ⅲ)要证明f(x)<x(0<x<1),只需证明f(xn)<xn,
法一:可证5(a1+a2+…+an)=[n+(5-n)](a1+a2+…+an)<nT,即可证明
法二:kn<1时,yn=(y1-y)+(y2-y1)+…+(yn-yn-1)
当kn≥1时,yn=y5-(y5-yn)=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]可证明
解答:(Ⅰ)解:
 ,…(2分)
,…(2分)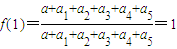 ; …(4分)
; …(4分)(Ⅱ)解:
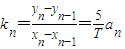 ,n=1,2,3,4,5. …(6分)
,n=1,2,3,4,5. …(6分)因为 a<a1<a2<a3<a4<a5,
所以 k1<k2<k3<k4<k5. …(8分)
(Ⅲ)证:由于f(x)的图象是连接各点Pn(xn,yn)(n=0,1,2,3,4,5)的折线,
要证明f(x)<x(0<x<1),只需证明f(xn)<xn(n=1,2,3,4).…(9分)
事实上,当x∈(xn-1,xn)时,
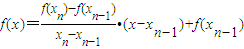 =
=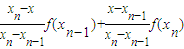
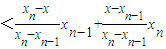 =x.
=x.下面证明f(xn)<xn.
法一:对任何n(n=1,2,3,4),5(a1+a2+…+an)=[n+(5-n)](a1+a2+…+an)…(10分)=n(a1+a2+…+an)+(5-n)(a1+a2+…+an)≤n(a1+a2+…+an)+(5-n)nan…(11分)=n[a1+a2+…+an+(5-n)an]<n(a1+a2+…+an+an+1+…+a5)=nT…(12分)
所以
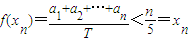 .…(13分)
.…(13分)法二:对任何n(n=1,2,3,4),
当kn<1时,yn=(y1-y)+(y2-y1)+…+(yn-yn-1)=
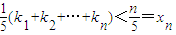 ;…(10分)
;…(10分)当kn≥1时,yn=y5-(y5-yn)=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]=
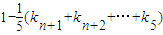
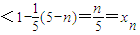 .
.综上,f(xn)<xn. …(13分)
点评:本题以新定义为载体,主要考查了数列的求和及一定的推理与运算的能力,试题具有一定的综合性

练习册系列答案
相关题目