题目内容
现有一组互不相同且从小到大排列的数据:a0,a1,a2,a3,a4,a5,其中a0=0.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记T=a0+a1+…+a5,xn=
,yn=
(a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2, …,5)的折线.(1)求f(0)和f(1)的值;
(2)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1、k2、k3、k4、k5的大小关系;
(3)证明当x∈(0,1)时,f(x)＜x.
思路解析:本题主要考查函数知识、斜率公式、分析问题解决问题的能力,结合已知采用分析法将所求问题转化到能够解决的范围内.
(1)解:f(0)==0,f(1)==1.
(2)解:kn=
,n=1,2, …,5,
因为a1＜a2＜a3＜a4＜a5,
所以k1＜k2＜k3＜k4＜k5.
(3)证明:由于f(x)的图象是连结各点Pn(xn,yn)(n=0,1, …,5)的折线,要证明f(x)＜x(0＜x＜1),只需证明f(xn)＜xn(n=1,2,3,4).事实上,当x∈(xn-1,xn)时,
f(x)=
(x-xn-1)+f(xn-1)
=
f(xn-1)+
f(xn)
＜
=x.
下面证明f(xn)＜xn.
对任何n(n=1,2,3,4),
5(a1+…+an)=［n+(5-n)］(a1+…+an)
=n(a1+…+an)+(5-n)(a1+…+an)
≤n(a1+…+an)+(5-n)nan=n［a1+…+an+(5-n)an］
＜n(a1+…+an+an+1+…+a5)=nT.
所以f(xn)=
＜
=xn.
练习册系列答案
阅读快车系列答案
相关题目
，yn=
（a0+a1+…+an），作函数y=f（x），使其图像为逐点依次连接点Pn（xn，yn）（n=0，1，2，…，5）的折线.
，
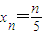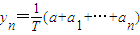（n=0，1，2，3，4，5），作函数y=f（x），使其图象为逐点依次连接点Pn（xn，yn）（n=0，1，2，3，4，5）的折线．