题目内容
设关于x的不等式x(x－a－1)＜0(a∈R)的解集为M，不等式x2－2x－3≤0的解集为N.
(1)当a＝1时，求集合M；
(2)若M∪N＝N，求实数a的取值范围．
（1）M＝{x|0＜x＜2}（2）[－2，2]
【解析】(1)当a＝1时，由已知得x(x－2)＜0，
解得0＜x＜2.所以M＝{x|0＜x＜2}．
(2)由已知得N＝{x|－1≤x≤3}．
①当a＜－1时，因为a＋1＜0，所以M＝{x|a＋1＜x＜0}．
由M∪N＝N，得M?N，所以－1≤a＋1＜0，解得－2≤a＜－1.
②当a＝－1时，M＝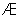
，显然有M?N，所以a＝－1成立．
③当a＞－1时，因为a＋1＞0，所以M＝{x|0＜x＜a＋1}．
因为M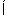
N，所以0＜a＋1≤3，解得－1＜a≤2.
综上所述，实数a的取值范围是[－2，2]．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
