题目内容
数列{an}是首项为1000,公比为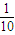 的等比数列,数列{bn}满足
的等比数列,数列{bn}满足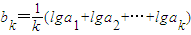 (k∈N*),
(k∈N*),(1)求数列{bn}的前n项和的最大值;
(2)求数列{|bn|}的前n项和Sn′.
【答案】分析:(1)首先写出数列{an}的通项公式得到数列{lgan}是首项为3,公差为-1的等差数列,即得到数列{bn}的通项公式假设第n为正,第n+1项为负解出n的值即可求出和的最大值;
(2)由(1)知当n≤7时,bn≥0,当n>7时,bn<0,分两种情况利用等差数列求和公式求出sn′即可.
解答:解:(1)由题意:an=104-n,∴lgan=4-n,
∴数列{lgan}是首项为3,公差为-1的等差数列,
∴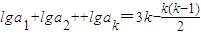 ,
,
∴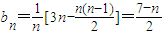
由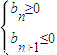 ,得6≤n≤7,
,得6≤n≤7,
∴数列{bn}的前n项和的最大值为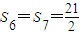
(2)由(1)当n≤7时,bn≥0,当n>7时,bn<0,
∴当n≤7时,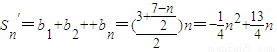
当n>7时,Sn′=b1+b2++b7-b8-b9--bn
=
∴Sn′=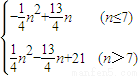 .
.
点评:考查学生灵活运用数列求和的公式,以及等差数列性质的运用能力.
(2)由(1)知当n≤7时,bn≥0,当n>7时,bn<0,分两种情况利用等差数列求和公式求出sn′即可.
解答:解:(1)由题意:an=104-n,∴lgan=4-n,
∴数列{lgan}是首项为3,公差为-1的等差数列,
∴
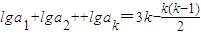 ,
,∴
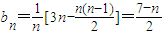
由
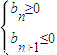 ,得6≤n≤7,
,得6≤n≤7,∴数列{bn}的前n项和的最大值为
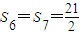
(2)由(1)当n≤7时,bn≥0,当n>7时,bn<0,
∴当n≤7时,
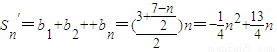
当n>7时,Sn′=b1+b2++b7-b8-b9--bn
=

∴Sn′=
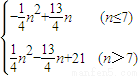 .
.点评:考查学生灵活运用数列求和的公式,以及等差数列性质的运用能力.

练习册系列答案
相关题目
如果一个数列的通项公式是an=k•qn(k,q为不等于零的常数)则下列说法中正确的是( )
| A、数列{an}是首项为k,公比为q的等比数列 | B、数列{an}是首项为kq,公比为q的等比数列 | C、数列{an}是首项为kq,公比为q-1的等比数列 | D、数列{an}不一定是等比数列 |