题目内容
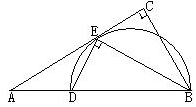
如图,在Rt△ABC中, , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,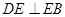 .
.
(Ⅰ)求证:AC是△BDE的外接圆的切线;
(Ⅱ)若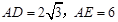 ,求EC的长.
,求EC的长.
(Ⅰ)取BD的中点O,连接OE.∠C=90°,得OE⊥AC,确定AC是△BDE的外接圆的切线.
(Ⅱ) EC=3.
解析试题分析:(Ⅰ)取BD的中点O,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,∴∠OBE=∠BEO,
∴∠CBE=∠BEO,∴BC∥OE. 3分
∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线. 5分
(Ⅱ)设⊙O的半径为r,则在△AOE中,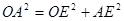 ,即
,即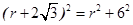 ,解得
,解得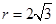 ,
,
∴OA=2OE, ∴∠A=30°,∠AOE=60°. ∴∠CBE=∠OBE=30°.
∴EC=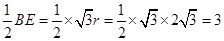 . 10分
. 10分
考点:平面几何选讲,圆的几何性质。
点评:中档题,本题作为选考内容,难度不大,正确解题的关键是,充分借助于几何图形的特征,利用“垂直关系”解题。

练习册系列答案
相关题目
 ,且AB是的
,且AB是的
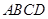 的外接圆为⊙
的外接圆为⊙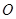 ,
,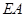 是⊙
是⊙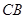 的延长线与
的延长线与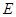 ,
,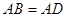 .
.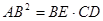 .
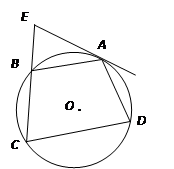
.
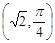 ,直线
,直线 的极坐标方程为
的极坐标方程为 ,且点A在直线
,且点A在直线 的值及直线
的值及直线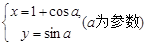 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系. 是圆
是圆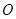 的直径,
的直径, 为圆上一点,
为圆上一点, ,垂足为
,垂足为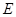 ,点
,点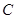 为圆
为圆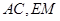 交于点
交于点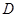 ,
,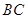 交
交 于点
于点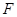 .
.
 ;(2)
;(2) .
. 外有一点
外有一点 ,作圆
,作圆 ,
, 为切点,过
为切点,过 ,作割线
,作割线 ,交圆于
,交圆于 、
、 两点,连接
两点,连接 并延长,交圆
并延长,交圆 ,连续
,连续 交圆
交圆 ,若
,若 .
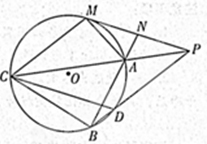
.
 ∽△
∽△ ;
; 是平行四边形.
是平行四边形. 的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,
的切线,A为切点,PBC是过点O的割线,PA=10,PB=5, 的平分线与BC和圆
的平分线与BC和圆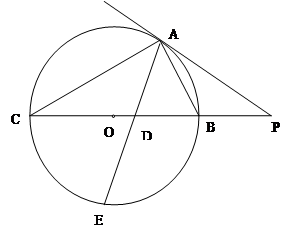
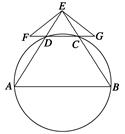
 ;
;
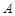 ,D为
,D为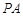 的中点,过点D引割线交⊙O于
的中点,过点D引割线交⊙O于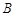 、
、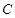 两点.
两点.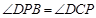 .
.