题目内容
已知点A1、A2分别是椭圆长轴的左、右顶点,M是椭圆上异于A1、A2的点,直线MA1、MA2分别与右准线l交于P、Q,F为右焦点.
求证:∠FQP+∠FPQ=![]() .
.
答案:
解析:
解析:
|
解:设椭圆 ∵M、A1、P三点共线, ∴ ∴y1= 同理可得y2= ∵kPF·kQF= = =-1 ∴∠PFQ= 分析:利用椭圆的参数方程设出点M的坐标,以减少变元. 点评:“点在曲线上”这一条件的使用方法有两种,一种是代数形式,如本题也可设M(x0,y0),但必须注意 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

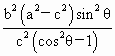 ·
·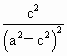
 (2012•辽宁)如图,已知椭圆C0:
(2012•辽宁)如图,已知椭圆C0: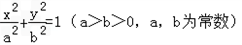 ,动圆C1:
,动圆C1: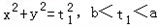 .点A1,A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点。
.点A1,A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点。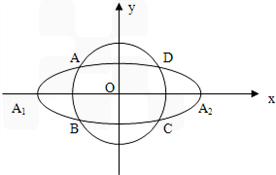
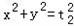 与C0相交于A',B',C',D'四点,其中b<t2<a,t1≠t2,若矩形ABCD与矩形A'B'C'D'的面积相等,证明:
与C0相交于A',B',C',D'四点,其中b<t2<a,t1≠t2,若矩形ABCD与矩形A'B'C'D'的面积相等,证明: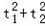 为定值。
为定值。 ,动圆C1:
,动圆C1: .点A1,A2分别为C的左右顶点,C1与C相交于A,B,C,D四点.
.点A1,A2分别为C的左右顶点,C1与C相交于A,B,C,D四点. 与C0相交于A',B',C',D'四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A'B'C'D'的面积相等,证明:
与C0相交于A',B',C',D'四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A'B'C'D'的面积相等,证明: 为定值.
为定值.