题目内容
如图,两块斜边长相等的直角三角板拼在一起.若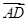 =x
=x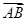 +y
+y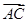 ,则x=________,y=________.
,则x=________,y=________.
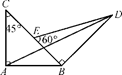
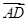 =x
=x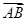 +y
+y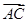 ,则x=________,y=________.
,则x=________,y=________.
x=1+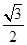 ,y=
,y=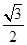
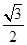 ,y=
,y=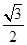
(解法1)以AB所在直线为x轴,以A为原点建立平面直角坐标系(如图).

令AB=2,则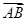 =(2,0),
=(2,0),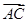 =(0,2),过D作DF⊥AB交AB的延长线为F,由已知得DF=BF=
=(0,2),过D作DF⊥AB交AB的延长线为F,由已知得DF=BF=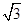 ,则
,则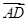 =(2+
=(2+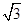 ,
,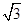 ).∵
).∵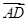 =x
=x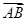 +y
+y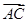 ,∴(2+
,∴(2+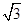 ,
,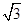 )=(2x,2y).
)=(2x,2y).
即有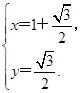
(解法2)
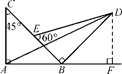
过D点作DF⊥AB交AB的延长线为F.由已知可求得BF=DF=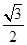 AB,
AB,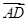 =
=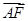 +
+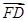 =
=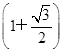
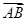 +
+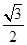
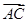 ,所以x=1+
,所以x=1+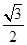 ,y=
,y=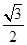 .
.

令AB=2,则
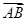 =(2,0),
=(2,0),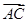 =(0,2),过D作DF⊥AB交AB的延长线为F,由已知得DF=BF=
=(0,2),过D作DF⊥AB交AB的延长线为F,由已知得DF=BF=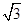 ,则
,则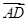 =(2+
=(2+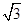 ,
,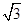 ).∵
).∵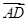 =x
=x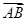 +y
+y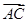 ,∴(2+
,∴(2+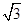 ,
,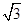 )=(2x,2y).
)=(2x,2y).即有
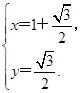
(解法2)

过D点作DF⊥AB交AB的延长线为F.由已知可求得BF=DF=
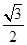 AB,
AB,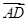 =
=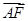 +
+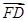 =
=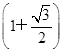
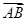 +
+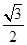
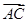 ,所以x=1+
,所以x=1+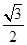 ,y=
,y=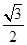 .
.
练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
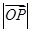 =1,
=1,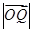 =
=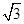 ,
,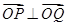 ,点
,点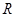 在
在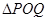 内,且
内,且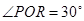 ,
,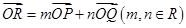 ,则
,则 等于( )
等于( )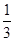
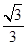
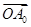 +
+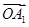 +…+OAn-1+
+…+OAn-1+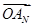 |等于( )
|等于( )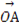 ⊥
⊥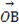 ,则向量
,则向量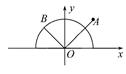
 ,
,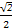 ,
, ,
,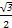 ,
,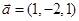 ,
,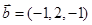 ;②
;②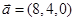 ,
,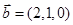 ;③
;③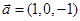 ,
,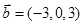 ;④
;④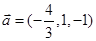 ,
,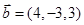
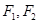 是双曲线
是双曲线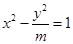 的两个焦点,过点
的两个焦点,过点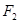 作与
作与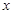 轴垂直的直线和双曲线的交点为
轴垂直的直线和双曲线的交点为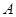 ,满足
,满足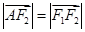 ,则
,则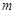 的值为 .
的值为 . ,
,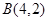 和向量
和向量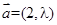 ,若
,若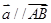 ,则实数
,则实数 的值为( )
的值为( )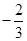
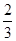

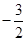
 为坐标原点,
为坐标原点,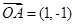 ,
,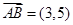 ,则点
,则点 的坐标为 ;
的坐标为 ;