题目内容
在△ABC中,已知a、b、c成等比数列,且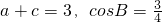 ,,则
,,则 =
=
- A.

- B.

- C.3
- D.-3
B
分析:先求a+c的平方,利用a、b、c成等比数列,结合余弦定理,求解ac的值,然后求解 .
.
解答:a+c=3,所以a2+c2+2ac=9…①
a、b、c成等比数列:b2=ac…②
由余弦定理:b2=a2+c2-2accosB…③
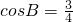 ,
,
解得ac=2,
 =-accosB=
=-accosB=
故选B.
点评:本题考查平面向量数量积的运算,等比数列的性质,余弦定理,考查学生分析问题解决问题的能力,是基础题.
分析:先求a+c的平方,利用a、b、c成等比数列,结合余弦定理,求解ac的值,然后求解
 .
.解答:a+c=3,所以a2+c2+2ac=9…①
a、b、c成等比数列:b2=ac…②
由余弦定理:b2=a2+c2-2accosB…③
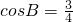 ,
,解得ac=2,
 =-accosB=
=-accosB=
故选B.
点评:本题考查平面向量数量积的运算,等比数列的性质,余弦定理,考查学生分析问题解决问题的能力,是基础题.

练习册系列答案
相关题目