题目内容
已知F1(-2,0),F2(2,0),点P满足|PF1|-|PF2|=2λ(λ为常数且0<λ≠2).(1)求P点的轨迹曲线E的方程;
(2)当0<λ<2时,过点M(-λ,0)作两直线l1、l2与曲线E相交于A、B两点,若MA·MB=0且AB恒过点F2(2,0)时,求λ的值.
解:(1)当λ>2时,不存在满足条件的P,λ=2时,P的轨迹方程为y=0(x≥2);
当0<λ<2时,P点的轨迹方程为![]() =1(x≥λ).
=1(x≥λ).
(讨论少一种情况扣1分)
(2)由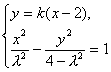 得
得![]() =1,
=1,
即(4-λ2)x2-λ2k2(x2-4x+4)-λ2(4-λ2)=0.
设A(x1,y1),B(x2,y2)
∴(4-λ2-λ2k2)x2+4λ2k2x-λ2(4k2+4-λ2)=0,
∴x1+x2=![]() ,
,
x1x2=![]() ,
,
y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4],
![]() =(x1+λ,y1),
=(x1+λ,y1),![]() =(x2+λ,y2),
=(x2+λ,y2),
![]() ·
·![]() =0
=0![]() (x1+λ)(x2+λ)+y1y2=0,即x1x2+λ(x1+x2)+λ2+y1y2=0.
(x1+λ)(x2+λ)+y1y2=0,即x1x2+λ(x1+x2)+λ2+y1y2=0.
∴x1x2+λ(x1+x2)+k2[x1x2-2(x1+x2)+4]+λ2=0.
∴![]() +4k2+λ2=0,
+4k2+λ2=0,
∴![]() =0,
=0,
16k2-4λ2k2-4λ2k4+4λ2-λ4-λ4k2+8λ2k4-4λ2k2-4λ2+λ4-4λ3k2-4λ2k4-4λ2k2+λ4k2=0,
化简得:k2(-4λ3-12λ2+16)=0.
∵对任意实数k等式恒成立,
∴λ3+3λ2-4=0,∴λ3-λ2+4λ2-4=0,
∴λ2(λ-1)+4(λ+1)(λ-1)=0,∴(λ-1)(λ2+4λ+4)=0,∴(λ-1)(λ+2)2=0,
∴0<λ<2,∴λ=1.
此时,P的轨迹方程为x2![]() =1(x≥1),当k不存在时,经验证也符合条件.
=1(x≥1),当k不存在时,经验证也符合条件.

练习册系列答案
相关题目
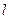 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线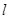 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线