题目内容
四面体ABCD中，AB、BC、BD两两互相垂直，且AB=BC=2，E是AC的中点，异面直线AD与BE所成角的大小是arccos
,求四面体ABCD的体积.
解析：以B为原点建立空间直角坐标系O—xyz,依题意有A（0,2,0）,C(2,0,0),E(1,1,0),设BD=m＞0,则D（0,0,m）.
∴
=(0,-2,m),
=(1,1,0),
·
=0×1+(-2)×1+m×0=-2,|
|=
,|
|=
,cos〈
,
〉=-
.
∴
=-
，解得m2=16.
∵m＞0,∴m=4.
∴V四面体ABCD=
·
·BD=
.
练习册系列答案
相关题目
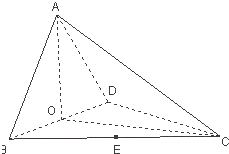如图，四面体ABCD中，O、E分别是BD、BC的中点，CA=CB=CD=BD=2，AB=AD=
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
=a, 
=b, 
=c,G为△BCD的重心，则
=__________.
= a，
= b，
= c，G∈平面ABC．则G为△ABC的重心的充分必要条件是
(a+b+c)；