题目内容
已知坐标平面内O为坐标原点,| OA |
| OB |
| OM |
| PA |
| PB |
| OP |
分析:由题意知
与
共线,由向量共线定理可得?λ∈[0,1]使得
=
=(λ,2λ),由向量数量积的坐标表示可得f(λ)=5λ2-20λ+12,λ∈[0,1]结合二次函数在区间[0,1]的单调性可求函数的最小值及P的坐标;代入向量夹角公式cos∠APB=
求值
| OM |
| OP |
| OP |
| λOM |
| ||||
|
|
解答:解:由题意,可设
=(λ,2λ),其中λ∈[0,1],
则
=(1-λ,5-2λ),
=(7-λ,1-2λ)(4分)
设f(λ)=
•
,则f(λ)=(1-λ)(7-λ)+(5-2λ)(1-2λ)
=5λ2-20λ+12,λ∈[0,1](8分)
又f(λ)在[0,1]上单调递减
∴当λ=1时f(λ)取得最小值,此时P点坐标为(1,2)(12分)
=(0,3),
=(6,-1)(14分)
∴cos∠APB=
=
=-
.(16分)
| OP |
则
| PA |
| PB |
设f(λ)=
| PA |
| PB |
=5λ2-20λ+12,λ∈[0,1](8分)
又f(λ)在[0,1]上单调递减
∴当λ=1时f(λ)取得最小值,此时P点坐标为(1,2)(12分)
| PA |
| PB |
∴cos∠APB=
| ||||
|
|
| -3 | ||
3
|
| ||
| 37 |
点评:本题考查平面向量共线定理,平面向量数量积的坐标表示,二次函数的单调性及最值的求解,向量夹角的坐标表示.熟练掌握向量的基础知识并能灵活运用是解决问题的关键.

练习册系列答案
相关题目
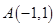 ,
, ,O为坐标原点,
,O为坐标原点,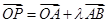 ,
, ,若点
,若点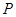 在第三象限内,则实数
在第三象限内,则实数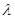 的取值范围是__________.
的取值范围是__________.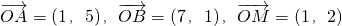 ,P是线段OM上一个动点.当
,P是线段OM上一个动点.当 取最小值时,求
取最小值时,求 的坐标,并求cos∠APB的值.
的坐标,并求cos∠APB的值.