题目内容
 (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
(Ⅰ) 求曲线E的方程;
(Ⅱ) 若点B1(x1,y1),B2(-1,y2),B3(x3,y3)在曲线E上,线段B1B3的垂直平分线为直线l,且|B1A|,|B2A|,|B3A|成等差数列,求x1+x3的值,并证明直线l过定点;
(Ⅲ)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足
| FG |
| FH |
分析:(Ⅰ)由
=2
,
•
=0.可知:NP为线段AM的垂直平分线,利用椭圆的椭圆可得:点N的轨迹是椭圆;
(II)利用椭圆的第二定义可得|B1A|,|B2A|,|B3A|的长度,利用成等差数列,即可得出x1+x3;由x1+x3=-2,可设线段B1B3的中点为(-1,t).于是
即可得到kB1B3,即可得到直线l的方程,进而得出过定点;
(III)把直线l的方程代入椭圆方程可得△>0即根与系数的关系,再利用向量相等即可得到λ与k的关系式,利用△>0即可得到λ的取值范围.
| AM |
| AP |
| NP |
| AM |
(II)利用椭圆的第二定义可得|B1A|,|B2A|,|B3A|的长度,利用成等差数列,即可得出x1+x3;由x1+x3=-2,可设线段B1B3的中点为(-1,t).于是
|
(III)把直线l的方程代入椭圆方程可得△>0即根与系数的关系,再利用向量相等即可得到λ与k的关系式,利用△>0即可得到λ的取值范围.
解答:解:(Ⅰ)由题意知,圆C的圆心为(-1,0),半径r=2
.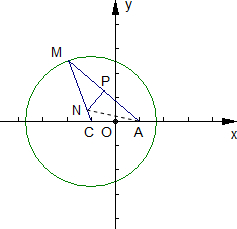
∵
=2
,
•
=0.
∴NP为线段AM的垂直平分线,∴|NA|=|NM|.
又∵|CN|+|NM|=r=2
,∴|CN|+|AN|=2
>2.
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点且长轴长为2
的椭圆. …(2分)
∴a=
,c=1,b=1.
∴曲线E的方程为
+y2=1. …(3分)
(Ⅱ)由(Ⅰ)知,A为椭圆的右焦点,其右准线方程为l1:x=2
设B1到直线l1的距离为d.
根据椭圆的定义知
=e=
,
得|B1A|=
d=
(2-x1)=
-
x1.
同理可得:|B2A|=
,|B3A|=
-
x3. …(5分)
∵|B1A|,|B2A|,|B3A|成等差数列,
∴|B1A|+|B3A|=2|B2A|,代入得x1+x3=-2. …(6分)
下面证明直线l过定点.
由x1+x3=-2,可设线段B1B3的中点为(-1,t).
∴
得kB1B3=
=
.
∴直线l的斜率k1=-2t,则直线l的方程为:y-t=-2t(x+1),
即l:2tx+y+t=0. …(8分)
∴直线l过定点,定点为(-
,0). …(9分)
(Ⅲ)当直线GH斜率存在时,设直线GH方程为y=kx+2,
代入椭圆
+y2=1,得(
+k2)x2+4kx+3=0.
由得k2>
. …(10分)
设G(x4,y4),H(x5,y5),则x4+x5=
,①
x4x5=
. ②
又∵
=λ
,∴(x4,y4-2)=λ(x5,y5).
∴x4=λx5. ③
由①②③联立得(
)2=x52=
,
即
=
,整理得
=
. …(12分)
∵k2>
,∴4<
<
,
∴4<
<
,解得
<λ<3且λ≠1.
又∵0<λ<1,∴
<λ<1. …(13分)
当直线GH斜率不存在时,直线GH方程为x=0,此时
=
,即λ=
.
∴
≤λ<1,即所求λ的取值范围是[
,1). …(14分)
| 2 |

∵
| AM |
| AP |
| NP |
| AM |
∴NP为线段AM的垂直平分线,∴|NA|=|NM|.
又∵|CN|+|NM|=r=2
| 2 |
| 2 |
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点且长轴长为2
| 2 |
∴a=
| 2 |
∴曲线E的方程为
| x2 |
| 2 |
(Ⅱ)由(Ⅰ)知,A为椭圆的右焦点,其右准线方程为l1:x=2
设B1到直线l1的距离为d.
根据椭圆的定义知
| |B1A| |
| d |
| 1 | ||
|
得|B1A|=
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
同理可得:|B2A|=
3
| ||
| 2 |
| 2 |
| ||
| 2 |
∵|B1A|,|B2A|,|B3A|成等差数列,
∴|B1A|+|B3A|=2|B2A|,代入得x1+x3=-2. …(6分)
下面证明直线l过定点.
由x1+x3=-2,可设线段B1B3的中点为(-1,t).
∴
|
| y1-y3 |
| x1-x3 |
| 1 |
| 2t |
∴直线l的斜率k1=-2t,则直线l的方程为:y-t=-2t(x+1),
即l:2tx+y+t=0. …(8分)
∴直线l过定点,定点为(-
| 1 |
| 2 |
(Ⅲ)当直线GH斜率存在时,设直线GH方程为y=kx+2,
代入椭圆
| x2 |
| 2 |
| 1 |
| 2 |
由得k2>
| 3 |
| 2 |
设G(x4,y4),H(x5,y5),则x4+x5=
| -4k | ||
|
x4x5=
| 3 | ||
|
又∵
| FG |
| FH |
∴x4=λx5. ③
由①②③联立得(
| x4+x5 |
| 1+λ |
| x4x5 |
| λ |
即
(
| ||||
| (1+λ)2 |
| ||||
| λ |
| 16 | ||
3(
|
| (1+λ)2 |
| λ |
∵k2>
| 3 |
| 2 |
| 16 | ||
|
| 16 |
| 3 |
∴4<
| (1+λ)2 |
| λ |
| 16 |
| 3 |
| 1 |
| 3 |
又∵0<λ<1,∴
| 1 |
| 3 |
当直线GH斜率不存在时,直线GH方程为x=0,此时
| FG |
| 1 |
| 3 |
| FH |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题综合考查了椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到△>0及根与系数的关系、线段垂直平分线的性质、中点坐标公式、等差数列的性质等基础知识与基本技能,考查了较强的计算能力、推理能力和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目