��Ŀ����
(��С������12��)��1�����ڶ����� �ϵĺ���
�ϵĺ��� ������
������ ����֤������
����֤������ ��
�� ���Ǽ�������
���Ǽ�������
��2�����������ж���1�������Ⲣ��ϵ�������⣺�� �Ƕ�����
�Ƕ����� �ϵĿɵ�����������
�ϵĿɵ����������� ����
���� ��
�� �ϵļ�������Ȼ����ս���һ���ձ黯�����⣺
�ϵļ�������Ȼ����ս���һ���ձ黯�����⣺
�� �Ƕ�����
�Ƕ����� �ϵĿɵ�������
�ϵĿɵ������� ����
����  +
+
 ��
��
��
�� �ϵļ�������
�ϵļ�������
ע��������ձ黯���Ǵӿ���һ��������ɵ����ǰ����ö����һ�����ϣ����ߴӿ���һ����С�ļ��Ϲ��ɵ����ǰ����ý�С���ϵĸ��ϡ�
��3��֤����2���н������ձ黯���⡣
���𰸡�
��1��֤������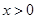 ʱ����
ʱ���� ����
����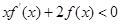 ����
����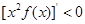 ���ԣ�����
���ԣ�����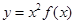 ��
��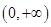 ���Ǽ�������������4��
���Ǽ�������������4��
��2���� �Ƕ�����
�Ƕ�����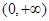 �ϵĿɵ�������
�ϵĿɵ�������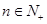 ����
����
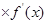 +
+ 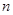
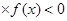 ����
���� 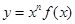 ��
��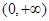 �ϵļ�������������.4��
�ϵļ�������������.4��
��3��֤���ԡ���������4��
����������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ