题目内容
(本小题满分13分) 已知抛物线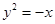 与直线
与直线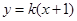 相交于
相交于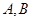 两点.
两点.
(1)求证:以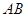 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点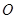 ;(2)当
;(2)当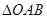 的面积等于
的面积等于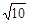 时,求
时,求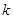 的值.
的值.
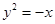 与直线
与直线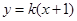 相交于
相交于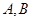 两点.
两点.(1)求证:以
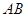 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点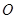 ;(2)当
;(2)当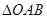 的面积等于
的面积等于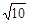 时,求
时,求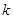 的值.
的值.(1)见解析(2)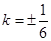
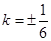
试题分析:(1)证明:由方程组
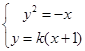 ,消去
,消去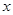 整理得:
整理得: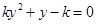 ,
,设
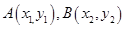 ,由韦达定理得:
,由韦达定理得: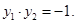
∵
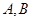 在抛物线
在抛物线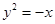 上,∴
上,∴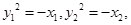
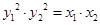 .
.∵
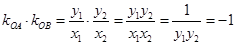 ,∴OA⊥OB.
,∴OA⊥OB. 故以
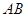 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点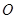 . ……6分
. ……6分(2)解:设直线与
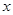 轴交于
轴交于 ,又显然
,又显然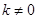 ,∴令
,∴令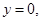 则
则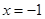 ,即
,即 (-1,0).
(-1,0).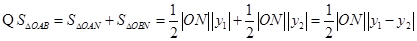 ,
,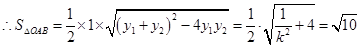 ,解得
,解得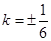 . ……13分
. ……13分点评:直线与圆锥曲线的相交问题一般是联立方程组,设而不求,借助根的判别式及根与系数的关系进行转化.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
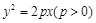 的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若
的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若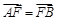 ,
,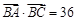 ,则抛物线的方程为 .
,则抛物线的方程为 . 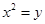 的准线方程是( )
的准线方程是( )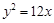 截直线
截直线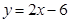 所得的弦长等于
所得的弦长等于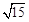
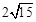
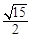
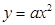 的准线方程是y=1,则此抛物线的标准方程为
的准线方程是y=1,则此抛物线的标准方程为  的焦点
的焦点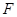 与点
与点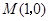 所得的线段与抛物线交于点
所得的线段与抛物线交于点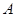 ,设点
,设点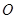 为坐标原点,则三角形
为坐标原点,则三角形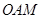 的面积为( )
的面积为( )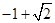
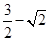
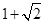
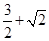
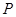 在抛物线
在抛物线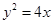 上,则点
上,则点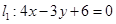 的距离和到直线
的距离和到直线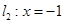 的距离之和的最小值为( )
的距离之和的最小值为( )
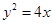 的焦点,且方向向量为
的焦点,且方向向量为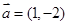 的直线
的直线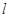 的方程是( )
的方程是( )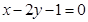
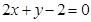
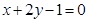
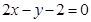
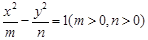 的离心率为2,有一个焦点与抛物线
的离心率为2,有一个焦点与抛物线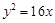 的焦点重合,则
的焦点重合,则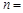 __________.
__________.