题目内容
求当m为何值时,f(x)=x2+2mx+3m+4.
(1)有且仅有一个零点;(2)有两个零点且均比-1大;
(1)有且仅有一个零点;(2)有两个零点且均比-1大;
(1) m=4或m=-1. (2) m的取值范围为(-5,-1)
本试题主要是考查了函数的零点,利用方程的解得到零点的证明。
(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根?Δ=0,解得。
(2)设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
利用韦达定理和判别式得到范围。
解 (1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根?Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,
∴m=4或m=-1. ……………… 5分
(2)设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
由题意,在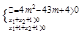 ?
?
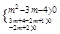 ?
?
∴-5<m<-1.故m的取值范围为(-5,-1).………………12分
(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根?Δ=0,解得。
(2)设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
利用韦达定理和判别式得到范围。
解 (1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根?Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,
∴m=4或m=-1. ……………… 5分
(2)设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
由题意,在
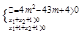 ?
?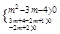 ?
?
∴-5<m<-1.故m的取值范围为(-5,-1).………………12分

练习册系列答案
相关题目
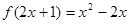 ,则
,则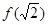 = _________
= _________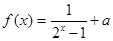 的图象关于原点对称,是a= 。
的图象关于原点对称,是a= 。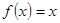 相等的是( )
相等的是( )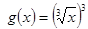
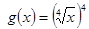
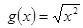
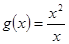
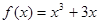 对任意的
对任意的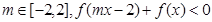 恒成立,
恒成立, .
.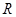 上的函数
上的函数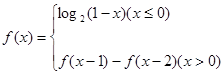 ,则
,则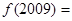 __________ .
__________ . 满足
满足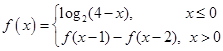 ,则
,则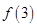 的值
的值