题目内容
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:

(1)完成被调查人员的频率分布直方图;
(2)若从年龄在 ,
, 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为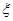 ,求随机变量
,求随机变量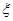 的分布列和数学期望.
的分布列和数学期望. 

(1)完成被调查人员的频率分布直方图;
(2)若从年龄在
 ,
, 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为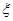 ,求随机变量
,求随机变量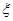 的分布列和数学期望.
的分布列和数学期望. 
(1)频率分布直方图详见解析;(2)分布列详见解析,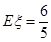 .
.
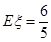 .
.试题分析:本题主要考查频率分布直方图和随机变量的分布列和数学期望等基础知识,考查学生分析问题解决问题的能力、画图的能力和计算能力.第一问,利用“
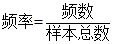 ”计算每一组的频率,再利用“
”计算每一组的频率,再利用“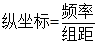 ”计算每一组的纵坐标,从而画出频率分布直方图;第二问,先通过对题意的分析,得出随机变量
”计算每一组的纵坐标,从而画出频率分布直方图;第二问,先通过对题意的分析,得出随机变量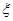 的所有可能取值,再对每一种情况求概率,列出分布列,利用
的所有可能取值,再对每一种情况求概率,列出分布列,利用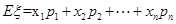 求数学期望.
求数学期望.试题解析:(Ⅰ)各组的频率分别是
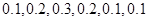 2分
2分所以图中各组的纵坐标分别是
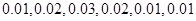 4分
4分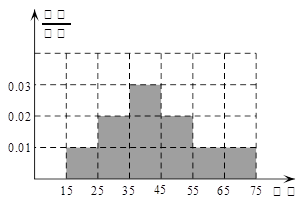 5分
5分(Ⅱ)
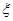 的所有可能取值为:0,1,2,3 6分
的所有可能取值为:0,1,2,3 6分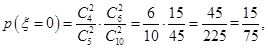
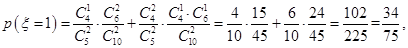
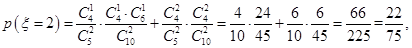
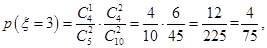 10分
10分所以
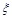 的分布列是:
的分布列是: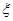 | 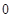 | 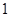 | 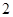 | 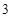 |
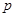 | 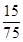 | 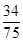 | 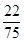 | 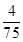 |
所以
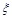 的数学期望
的数学期望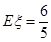 12分
12分
练习册系列答案
相关题目
 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.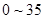





 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
天的
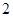 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求


 名编号为
名编号为 的球员进行足球点球练习,每人点球
的球员进行足球点球练习,每人点球 次,射中的次数如下表:
次,射中的次数如下表: .
. 次综合测评中的成绩的茎叶图,其中一个数字被污损;则甲的平均成绩超过乙的平均成绩的概率为 .
次综合测评中的成绩的茎叶图,其中一个数字被污损;则甲的平均成绩超过乙的平均成绩的概率为 .

 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个
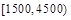 元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.
元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.