题目内容
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )A.
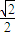
B.

C.
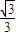
D.
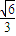
【答案】分析:由题意,利用方程的思想,先设出侧棱长为l,正三棱锥的底边长为a,利用异面直线所成角的概念及已知的所成角为45°建立l和a的方程,解出棱长l用a表示,在利用直线与平面所成角的概念求出所要求得线面角.
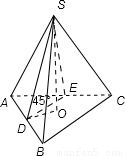
解答:解:由题义画出以下图形:由于三棱锥S-ABC为正三棱锥,设侧棱为l,底面边长为a,因为D是AB的中点,且SD与BC成45°角,如图取AC的中点E,因为DE∥BC,所以∠SDE=45°,在直角三角形SDE可以建立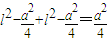 ⇒
⇒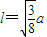 ,在直角三角形SOD中,OD=
,在直角三角形SOD中,OD=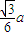 ,SD=
,SD=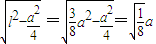 ,SO=
,SO=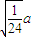 ,所以直线ssssSD与平面ABC所成的线面角即为∠SDO,所以SD与底面ABC所成角的正弦值为sin
,所以直线ssssSD与平面ABC所成的线面角即为∠SDO,所以SD与底面ABC所成角的正弦值为sin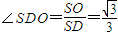 ,
,
故答案为:C
点评:此题重点考查了异面直线所成角的概念,还考查了直线与平面所成的线面角的概念及解题过程中方程的解题思想.
解答:解:由题义画出以下图形:由于三棱锥S-ABC为正三棱锥,设侧棱为l,底面边长为a,因为D是AB的中点,且SD与BC成45°角,如图取AC的中点E,因为DE∥BC,所以∠SDE=45°,在直角三角形SDE可以建立
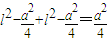 ⇒
⇒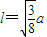 ,在直角三角形SOD中,OD=
,在直角三角形SOD中,OD=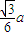 ,SD=
,SD=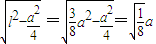 ,SO=
,SO=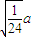 ,所以直线ssssSD与平面ABC所成的线面角即为∠SDO,所以SD与底面ABC所成角的正弦值为sin
,所以直线ssssSD与平面ABC所成的线面角即为∠SDO,所以SD与底面ABC所成角的正弦值为sin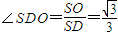 ,
,故答案为:C

点评:此题重点考查了异面直线所成角的概念,还考查了直线与平面所成的线面角的概念及解题过程中方程的解题思想.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
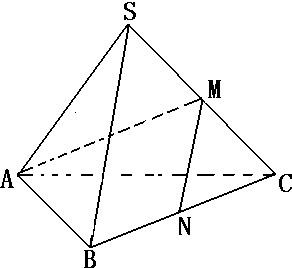 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|