题目内容
已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，且a、b满足关系|ka＋b|＝
|a－kb|，(k为正实数)
(1)求证：(a＋b)⊥(a－b)；
(2)求将a与b的数量积表示为关于k的函数f(k)．
答案：
解析：
解析：
|
(1)证明：由a＝(cosα，sinα)，b＝(cosβ，sinβ)，则(a＋b)·(a－b)＝a2－b2＝|a|2－|b|2＝1－1＝0， ∴(a＋b)⊥(a－b)． (2)解：∵|ka＋b|＝ ∴(ka＋b)2＝3(a－kb)2， 即k2a2＋2ka·b＋b2＝3a2＋3k2b2－6ka·b． 又a2＝cos2α＋sin2α＝1，b2＝cos2β＋sin2β＝1． 故k2＋2ka·b＋1＝3－6ka·b＋3k2， 由此得a·b＝ |
|a－kB|，
，故f(k)＝
(k＞0)．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
，－1)，则|2a－b|的最大值、最小值分别是________．
，－1)，则|2a－b|的最大值是________．
.
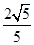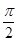<β<0<α<
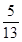，求sinα的值．