题目内容
已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，|a－b|＝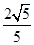
.
(1)求cos(α－β)的值；
(2)若－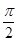
<β<0<α<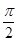，且sinβ＝－
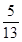，求sinα的值．
【答案】
（1）cos(α－β)＝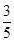
.（2）
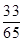
【解析】(1)∵|a－b|＝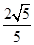
，∴a2－2a·b＋b2＝
，
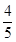又a＝(cosα，sinα)，b＝(cosβ，sinβ)，
∴a2＝b2＝1，a·b＝cosαcosβ＋sinαsinβ＝cos(α－β)，
∴cos(α－β)＝.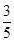
(2)∵－
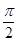<β<0<α<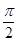，∴0<α－β<π，
由(1)得cos(α－β)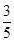＝，∴sin(α－β)＝，
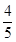又sinβ＝－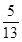
，∴cosβ＝
，
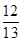∴sinα＝sin[(α－β)＋β]
＝sin(α－β)cosβ＋cos(α－β)sinβ
＝×＋×
＝.
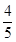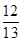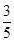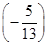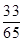练习册系列答案
相关题目
，－1)，则|2a－b|的最大值、最小值分别是________．
，－1)，则|2a－b|的最大值是________．