题目内容
1.已知抛物线y2=4x的焦点为F,与y轴相切的圆C过点F并与抛物线交于点M,且|MF|=2,则圆C的面积为( )| A. | 2π | B. | π | C. | 3π | D. | 4π |
分析 先求出M的坐标,可得MF的方程,再建立方程,求出圆的半径,即可得出结论.
解答 解:抛物线y2=4x的焦点为F(1,0).
∵圆C与抛物线交于点M,且|MF|=2,
∴M的横坐标为1,∴M(1,2)或(1,-2)
取M(1,2),则直线MF的方程为x=1,
设圆的半径为r,则r+$\sqrt{{r}^{2}-1}$=1,
∴r=1,
∴圆C的面积为π.
故选:B.
点评 本题考查直线与圆,圆与抛物线的位置关系,考查学生分析解决问题的能力,确定M的坐标是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
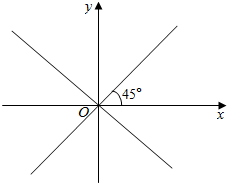
12.如图,终边落在直线y=±x上的角α的集合是( )

| A. | {α|α=k•360°+45°,k∈Z} | B. | {α|α=k•180°+45°,k∈Z} | ||
| C. | {α|α=k•180°-45°,k∈Z} | D. | {α|α=k•90°+45°,k∈Z} |
13.下列各函数中,为指数函数的是( )
| A. | y=(-1.3)x | B. | y=${(\frac{1}{2})}^{x}$ | C. | y=x2 | D. | y=x-1 |
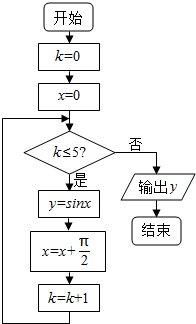
10.如图所示的程序框图,它的输出结果是( )

| A. | -1 | B. | 0 | C. | 1 | D. | 16 |
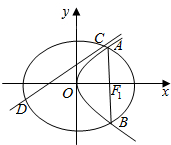 已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和抛物线y2=2px(p>0)相交于A、B两点,直线AB过抛物线的焦点F1,且|AB|=8,椭圆的离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和抛物线y2=2px(p>0)相交于A、B两点,直线AB过抛物线的焦点F1,且|AB|=8,椭圆的离心率为$\frac{\sqrt{2}}{2}$.