题目内容
10.(Ⅰ)已知集合A={|a+1|,3,5},B={2a+1,a2a+2,a2+2a-1},若A∩B={2,3},求实数a的值.(Ⅱ)已知集合A=(-1,2),B=(a,2-a),若B⊆A,求实数a的范围.
分析 (Ⅰ)根据A与B,以及A与B的交集,确定出a的范围即可;
(Ⅱ)由A,B,以及B为A的子集,求出a的范围即可.
解答 解:(Ⅰ)∵A={|a+1|,3,5},B={2a+1,a2a+2,a2+2a-1},且A∩B={2,3},
∴|a+1|=2,即a+1=2或a+1=-2,
解得:a=1或a=-3,
当a=1时,A={2,3,5},B={3,1,2},不合题意,舍去;
当a=-3时,A={2,3,5},B={-5,$\frac{1}{81}$,2},符合题意,
则实数a的值为-3;
(Ⅱ)∵A=(-1,2),B=(a,2-a),且B⊆A,
∴当B=∅,即a≥2-a时,解得:a≥1,满足题意;
当B≠∅,即a<2-a时,解得:a<1,
则有$\left\{\begin{array}{l}{a≥-1}\\{2-a≤2}\end{array}\right.$,解得:0≤a<1,
综上,实数a的范围是a≥0.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.已知抛物线y2=4x的焦点为F,与y轴相切的圆C过点F并与抛物线交于点M,且|MF|=2,则圆C的面积为( )
| A. | 2π | B. | π | C. | 3π | D. | 4π |
 已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥DC,DC的延长线交PQ于点Q.
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥DC,DC的延长线交PQ于点Q.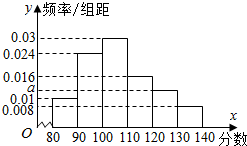 某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.
某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.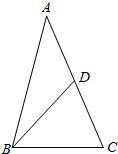 已知△ABC中,D为AC的中点,AB=3,BD=2,cos∠ABC=$\frac{1}{4}$.
已知△ABC中,D为AC的中点,AB=3,BD=2,cos∠ABC=$\frac{1}{4}$.