题目内容
已知数列{an}的前n项和为Sn,且满足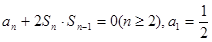
(Ⅰ)求证:{ }是等差数列;
}是等差数列;
(Ⅱ)求an的表达式
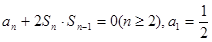
(Ⅰ)求证:{
 }是等差数列;
}是等差数列;(Ⅱ)求an的表达式
(Ⅰ)证明略
(Ⅱ)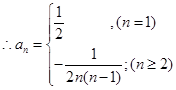
(Ⅱ)
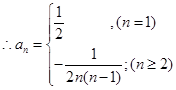
本试题主要是考查了数列的通项公式的求解,数列的定义的运用。
(1)因为数列{an}的前n项和为Sn,且满足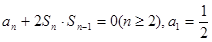 ,借助于关系式,
,借助于关系式,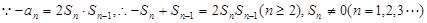 得到
得到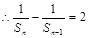 ,从而证明
,从而证明
(2)由(1)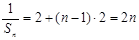
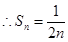
当n≥2时,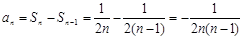 ,验证当n=1时是否满足即可,最后写出结论。
,验证当n=1时是否满足即可,最后写出结论。
(1)因为数列{an}的前n项和为Sn,且满足
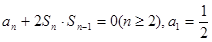 ,借助于关系式,
,借助于关系式,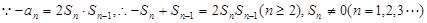 得到
得到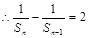 ,从而证明
,从而证明(2)由(1)
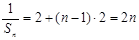
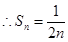
当n≥2时,
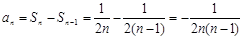 ,验证当n=1时是否满足即可,最后写出结论。
,验证当n=1时是否满足即可,最后写出结论。
练习册系列答案
相关题目
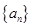 中的相邻两项
中的相邻两项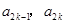 是关于
是关于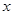 的方程
的方程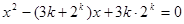 的两个根,且
的两个根,且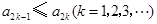 .
.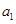 ,
,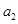 ,
,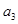 ,
,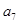 ;
; 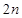 项和
项和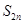 ;
;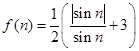 ,
,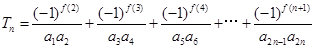 ,
,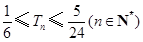 .
.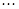
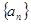 是公差不为0的等差数列,
是公差不为0的等差数列,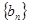 是等比数列,且
是等比数列,且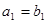 ,
,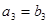 ,
,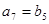 ,
,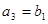
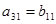
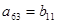
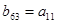
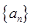 满足
满足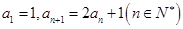
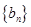 满足
满足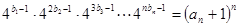 ,求数列
,求数列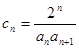 ,求数列
,求数列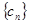 的前n项和
的前n项和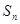
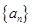 中,
中,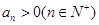 ,公比
,公比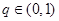 ,且
,且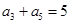 ,又
,又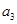 与
与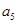 的等比中项为2.
的等比中项为2.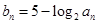 ,数列
,数列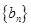 的前
的前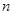 项和为
项和为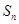 ,求数列
,求数列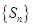 的通项公式;
的通项公式;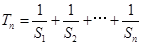 ,求
,求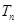 .
.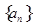 的前
的前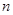 项和为
项和为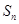 ,且
,且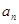 是
是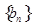 中,
中,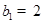 ,点
,点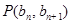 在直线
在直线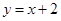 上.
上.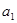 和
和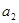 的值;
的值;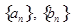 的通项
的通项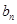 ;
;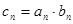 ,求数列
,求数列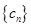 的前n项和
的前n项和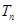 .
.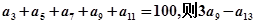 的值为( )
的值为( )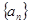 中,
中,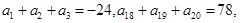 则此数列的前
则此数列的前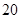 项和 _________.
项和 _________.