题目内容
 (2007•温州一模)如图,设A(-2,0),B(2,0),直线l:x=1,点C在直线l上,动点P在直线BC上,且满足
(2007•温州一模)如图,设A(-2,0),B(2,0),直线l:x=1,点C在直线l上,动点P在直线BC上,且满足| AP |
| AC |
(Ⅰ)若点C的纵坐标为1,求点P的坐标;
(Ⅱ)求点P的轨迹方程.
分析:(I)设出P点坐标为(x,y),根据A(-2,0),B(2,0),C(1,1)我们可求出
=(x+2,y),
=(3,1),进而根据
•
=0,P点在BC上,结合向量数量的公式,构造x,y的方程组,解方程组,即可求出P点坐标.
(II)设P(x,y),C(1,h),由已知可得
=(x+2,y),
=(3,h),
=(x-1,y-h),
=(-1,h)进而根据
•
=0,P点在BC上,结合向量数量的公式,构造x,y,h的方程组,消掉h后,即可得到点P的轨迹E的方程.
| AP |
| AC |
| AP |
| AC |
(II)设P(x,y),C(1,h),由已知可得
| AP |
| AC |
| CP |
| BC |
| AP |
| AC |
解答:解:(I)设P(x,y),则
=(x+2,y),
=(3,1),
=(x-1,y-1),
=(-1,1)
由题意得:y+x-2=0,y+3(x+2)=0,则x=-4,y=6,即点P的坐标为(-4,6)
(II)设P(x,y),C(1,h),
=(x+2,y),
=(3,h),
=(x-1,y-h),
=(-1,h)
则由题意得:y+h(x-2)=0,hy+3(x+2)=0,---(10分)
消去h得点P的轨迹E的方程为
-
=1.---(14分)
| AP |
| AC |
| CP |
| BC |
由题意得:y+x-2=0,y+3(x+2)=0,则x=-4,y=6,即点P的坐标为(-4,6)
(II)设P(x,y),C(1,h),
| AP |
| AC |
| CP |
| BC |
则由题意得:y+h(x-2)=0,hy+3(x+2)=0,---(10分)
消去h得点P的轨迹E的方程为
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题考查的知识点是数量积判断两个平面向量的垂直关系,轨迹方程,其中(2)中熟练掌握利用坐标法,求轨迹方程的方法和步骤,是解答此类问题的关键.

练习册系列答案
相关题目
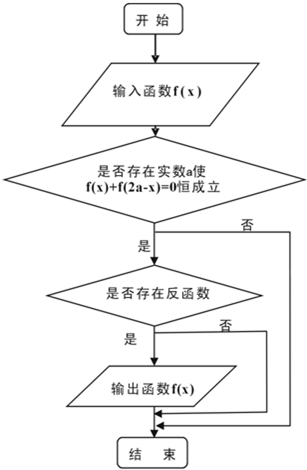 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )