题目内容
(本小题满分13分)已知圆G:x2+y2—2x—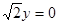 ,经过椭圆
,经过椭圆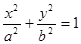 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为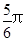 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.
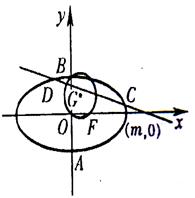
(Ⅰ)求椭圆方程
(Ⅱ)当右焦点在以线段CD为直径的圆E的内部,求实数m的范围
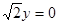 ,经过椭圆
,经过椭圆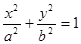 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为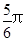 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.
(Ⅰ)求椭圆方程
(Ⅱ)当右焦点在以线段CD为直径的圆E的内部,求实数m的范围
(Ⅰ)椭圆方程为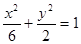 ;(Ⅱ)实数m的取值范围为(
;(Ⅱ)实数m的取值范围为( ,3)。
,3)。
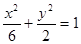 ;(Ⅱ)实数m的取值范围为(
;(Ⅱ)实数m的取值范围为( ,3)。
,3)。本试题主要是考查了椭圆的方程的求解,以及圆与椭圆的位置关系的运用。
(1)因为圆G经过点F、B ∴F(2,0),B(0,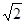 )
)
∴椭圆的焦半径c=2,短半轴长b=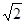 ∴a2=b2+o2=6
∴a2=b2+o2=6
得到椭圆的方程。
(2)设直线l的方程为y=-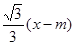 (m>
(m> )
)
然后直线与椭圆方程联立,借助于韦达定理和向量的数量积得到实数m的范围。
(Ⅰ)∵圆G经过点F、B ∴F(2,0),B(0,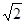 )
)
∴椭圆的焦半径c=2,短半轴长b=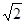 ∴a2=b2+o2=6
∴a2=b2+o2=6
故椭圆方程为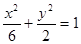 …………………………4分
…………………………4分
(Ⅱ)设直线l的方程为y=-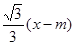 (m>
(m> )
)
由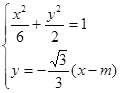
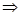 2x2-2mx+(m2-6)=0
2x2-2mx+(m2-6)=0
由△=4m2-8(m2-6)>0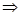 m2<12
m2<12
∴-2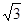 <m<2
<m<2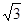 ………………………………………6分
………………………………………6分
又m> ∴
∴ <m<2
<m<2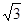 ……………………………………7分
……………………………………7分
设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=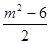
∴y1·y2=[-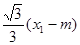 ][-
][-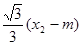 ]=
]=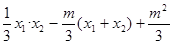
∵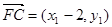
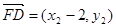
 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=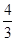 x1x2-
x1x2-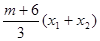 +
+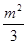 +4
+4
=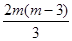 ……………………………………10分
……………………………………10分
∵点F在圆E内部 ∴ <0
<0
即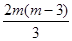 <0
<0 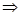 0<m<3
0<m<3
又∵ <m<2
<m<2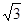
∴实数m的取值范围为( ,3)………………………………13分
,3)………………………………13分
(1)因为圆G经过点F、B ∴F(2,0),B(0,
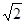 )
)∴椭圆的焦半径c=2,短半轴长b=
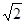 ∴a2=b2+o2=6
∴a2=b2+o2=6得到椭圆的方程。
(2)设直线l的方程为y=-
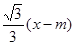 (m>
(m> )
)然后直线与椭圆方程联立,借助于韦达定理和向量的数量积得到实数m的范围。
(Ⅰ)∵圆G经过点F、B ∴F(2,0),B(0,
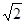 )
)∴椭圆的焦半径c=2,短半轴长b=
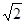 ∴a2=b2+o2=6
∴a2=b2+o2=6故椭圆方程为
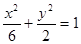 …………………………4分
…………………………4分(Ⅱ)设直线l的方程为y=-
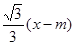 (m>
(m> )
)由
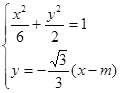
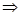 2x2-2mx+(m2-6)=0
2x2-2mx+(m2-6)=0由△=4m2-8(m2-6)>0
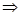 m2<12
m2<12 ∴-2
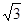 <m<2
<m<2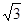 ………………………………………6分
………………………………………6分又m>
 ∴
∴ <m<2
<m<2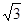 ……………………………………7分
……………………………………7分设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=
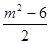
∴y1·y2=[-
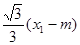 ][-
][-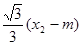 ]=
]=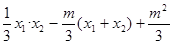
∵
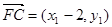
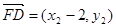
 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2=
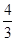 x1x2-
x1x2-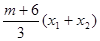 +
+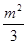 +4
+4=
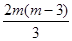 ……………………………………10分
……………………………………10分∵点F在圆E内部 ∴
 <0
<0即
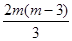 <0
<0 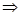 0<m<3
0<m<3又∵
 <m<2
<m<2
∴实数m的取值范围为(
 ,3)………………………………13分
,3)………………………………13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
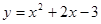 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。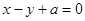 截得的弦长为
截得的弦长为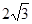 ,求
,求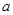 的值。
的值。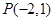 且被圆C:
且被圆C: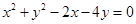 截得弦最长的直线l的方程是( )
截得弦最长的直线l的方程是( ) 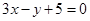
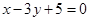
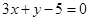
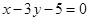
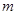 、
、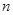 ,则直线
,则直线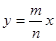 与圆
与圆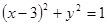 相交的概率是( )
相交的概率是( )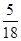
 的顶点在坐标原点,准线
的顶点在坐标原点,准线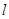 的方程为
的方程为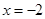 ,点
,点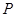 在准线
在准线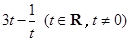 ,点
,点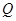 在
在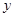 轴上,纵坐标为
轴上,纵坐标为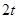 .
.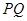 恒与一个圆心在
恒与一个圆心在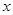 轴上的定圆
轴上的定圆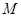 相切,并求出圆
相切,并求出圆 (
( 为参数)的倾斜角的大小.
为参数)的倾斜角的大小.  ,
, 是曲线
是曲线 上任意一点,求
上任意一点,求 的面积的最小值.
的面积的最小值.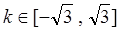 ,直线
,直线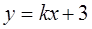 与圆
与圆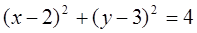 相交于M、N两点,则|MN|
相交于M、N两点,则|MN|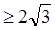 的概率为
的概率为 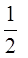
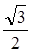
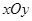 中,圆
中,圆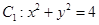 ,圆
,圆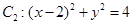 。
。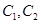 的极坐标方程,并求出圆
的极坐标方程,并求出圆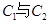 的公共弦的参数方程。
的公共弦的参数方程。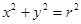 与直线
与直线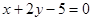 相交于
相交于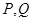 两点, 若
两点, 若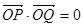 (
(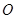 为原点),则圆的半径
为原点),则圆的半径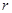 值的为 ;
值的为 ;