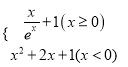题目内容
【题目】函数
有两个零点，则
的取值范围为（ ）
A.
B.
C.
D.
【答案】A
【解析】
要使函数f(x)=xln x- m有两个零点,即xlnx=m有两个不同的根,即函数y= g (x)的图像与直线y = m的图像有两个不同的交点，设g(x)= xln x，对其求导分析单调性，进而表示极小值，再由极限思想考虑端点值，最后由数形结合思想观察图象得答案.
函数的定义域为(0, +∞)，由f(x)=xlnx一m=0，得xlnx=m,
设g(x)=xlnx，则g'(x)=lnx+1,
由g'(x)>0，得
，此时函数g (x)单调递增;
由g'(x)<0,得0<x<
，此时函数g(x)单调递减;
即当x=时，函数g (x)取得极小值
当x→0，g(x)→0；当x→+∞，g(x)→十∞，
所以要使函数f(x)=xlnx-m有两个零点,即xlnx=m有两个不同的根,即函数y=g(x)的图像与直线y=m的图像有两个不同的交点，
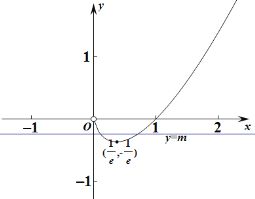
则-< m< 0，
故选：A
练习册系列答案
相关题目
【题目】4月23日是“世界读书日”，某中学开展了一系列的读书教育活动．学校为了解高三学生课外阅读情况，采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组（每名学生只能参加一个读书小组）学生抽取12名学生参加问卷调查．各组人数统计如下：
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
（1）从参加问卷调查的12名学生中随机抽取2人，求这2人来自同一个小组的概率；
（2）从已抽取的甲、丙两个小组的学生中随机抽取2人，用
表示抽得甲组学生的人数，求随机变量的分布列和数学期望．
